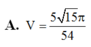
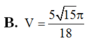
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có: O là giao điểm của trục đường tròn ngoại tiếp tam giác ABC và SAB.
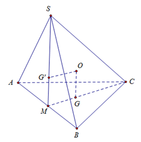
Ta có: O G = 1 3 S M = 3 6 ; M G = C M 3 = 3 6
R = S O = M G 2 + S G 2 = 3 6 + 1 3 = 15 6
Cách 2: Áp dụng CT giải nhanh trong trường hợp S A B ⊥ A B C ta có:
R 2 = R 2 A B C + R 2 S A B − A B 2 4 = 1 2 3 + 1 2 3 − 1 4 = 2 3 − 1 4 = 5 12 ⇒ R = 15 6 .
Vậy V = 4 3 π R 3 = 5 15 π 54 .
Đáp án A
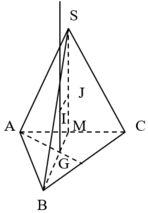
SM = M B tan 60 0 = 3 6
IG = x ⇒ JM = IG ⇒ SI = 1 12 + ( 3 6 + x ) 2 , IA = 1 3 + x 2
SI = IA ⇒ x 2 + 1 4 = ( x 2 + 3 3 x + 1 2 ) ⇒ x = 1 2 3 ⇒ R = 5 12
V = 4 3 πR 3 = 5 15 π 54
Đáp án B.
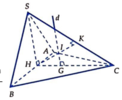
Gọi H là trung điểm AB, G là trọng tâm tam giác ABC, K là trung điểm SC.
Ta có: 
SH = SC => HK là trung trực SC. Qua O kẻ trục d//SH => d ⊥ (ABC)
Gọi
=> I là tâm mặt cầu ngoại tiếp hình chóp SABC
Ta có
Xét ∆ HIG vuông tại G:
Vậy thể tích khối cầu ngoại tiếp hình chóp
.Thể tích V của khối cầu ngoại tiếp hình chóp đã cho bằng
