Cho tứ diện ABCD. G là trọng tâm tam giác BCD. Tìm giao tuyến của hai mặt phẳng (ACD) và (GAB).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
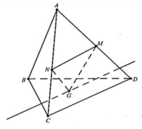
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: ![]()
Khi đó: Giao tuyến = ![]() = Gx // CD
= Gx // CD

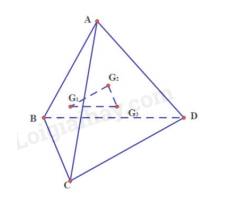
a) Gọi E, F, H là trung điểm của BC, CD, BD
Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\)
\({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\)
Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\)
Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\)
Tương tự ta có:\({G_2}{G_3}//(BCD)\)
Do đó, \({G_1}{G_2}{G_3}//(BCD)\)
b) Ta có: \({G_1}{G_2}{G_3}//(BCD)\) nên \({G_1}{G_2} // BD\)
mà \({G_3}\) là điểm chung của hai mặt phẳng
Từ \({G_3}\) kẻ \({G_3}x\) sao cho \({G_3}x//BD\)
Vậy \({G_3}x\) là giao tuyến cần tìm.

 phần c là hỏi về thiết diện của tứ diện ABCD cắt bởi (AG1G2) đk bn ???🤔
phần c là hỏi về thiết diện của tứ diện ABCD cắt bởi (AG1G2) đk bn ???🤔

\(BG\) cắt \(AD\) tại \(K\), \(BM\) cắt \(AC\) tại \(C\).
Giao tuyển của hai mặt phẳng \(\left(BGM\right)\) và \(\left(ACD\right)\) là \(CK\).

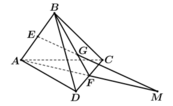


Chọn B.