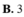
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Phương trình hoành độ giao điểm là: m x 3 - x 2 2 x + 8 m = 0
⇔ m x + 2 x 2 - 2 x + 4 - x x + 2 = 0 ⇔ x + 2 m x 2 - 2 m x + 4 m - x = 0 ⇔ [ x = - 2 g x = m x 2 - 1 + 2 m x + 4 m = 0
Để đồ thị C m cắt trục hoành tại ba điểm phân biệt thì g x = 0 có 2 nghiệm phân biệt khác -2 ⇔ m ≠ 0 ∆ = 1 + 2 m 2 - 16 m 2 > 0 g - 2 = 4 m + 2 1 + 2 m + 4 m ≠ 0 ⇔ m ∈ - 1 6 ; 1 2 \ 0
Chọn B.
Phương trình hoành độ giao điểm:
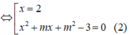
Để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình (1) có ba nghiệm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt khác 2
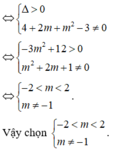
Phương trình hoành độ giao điểm của (C) và đường thẳng d:
1 3 x 3 - m x 2 - x + m + 2 3 = 0 ⇔ ( x - 1 ) x 2 + ( - 3 m + 1 ) x - 3 m - 2 = 0
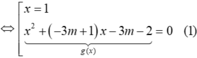
(C) cắt Ox tại ba điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt khác 1
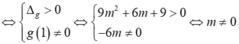
Gọi x1= 1 còn x2; x3 là nghiệm phương trình (1) nên theo Viet ta có
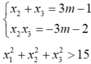
Chọn A.
Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
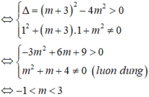
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
