Có năm đoạn thẳng có độ dài lần lượt là 1cm, 2c, 3cm, 4cm, 5cm. Lấy ngẫu nhiên ra ba đoạn thẳng, tính xác suất để ba đoạn thẳng được chọn ra là độ dài ba cạnh của một tam giác.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
Lấy ba đoạn thẳng từ năm đoạn thẳng có
C
5
3
= 10 cách. Suy ra số phần tử của không gian mẫu là ![]()
Gọi A là biến cố: " Ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác ".
Khi đó 3 đoạn thẳng được chọn thỏa mãn tính chất: Tổng độ dài 2 đoạn thẳng luôn lớn hơn độ dài đoạn thẳng còn lại.
Có 3 bộ thỏa mãn là ![]()
Vậy xác suất để ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác là
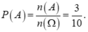

Ta có: 1 = 3 - 2 = 4 - 3 = 5 - 4
Suy ra: trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.
* Nếu cạnh nhỏ nhất là 2cm
Ta có: 4 - 3 < 2 < 4 + 3; 5 - 4 < 2 < 5 + 4
Suy ra: hai cạnh kia là 3cm và 4cm hoặc 4cm và 5cm
* Nếu cạnh nhỏ nhất là 3cm
Ta có: 5 - 4 < 3 < 5 + 4; 3 = 5 - 2; 3 > 4 - 2
Như vậy hai cạnh kia là 5cm và 4cm
* Không có trường hợp cạnh nhỏ nhất là 4cm
Vậy có thể vẽ được ba tam giác với độ dài các cạnh là:
2cm; 3cm; 4cm
2cm; 4cm; 5cm
3cm; 4cm; 5cm

Trong một tam giác, độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng của hai cạnh còn lại.
Vậy nên với năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm ta dựng được tam giác với ba cạnh là các đoạn thẳng có độ dài là:
+ Bộ ba 2cm, 3cm, 4cm (3-2 < 4 < 3+2)
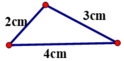
Dựng đoạn thẳng bằng 4cm.
Từ hai đầu đoạn thẳng dựng các cung tròn bán kính lần lượt 2cm và 3cm.
Hai cung tròn này cắt nhau tại điểm thứ 3.
Nối các điểm ta được tam giác cần dựng.
+ Bộ ba 3cm, 4cm, 5cm (4-3 < 5 < 4+3)
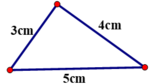
Dựng đoạn thẳng bằng 4cm.
Dựng đoạn thẳng bằng 5cm.
Từ hai đầu đoạn thẳng dựng các cung tròn bán kính lần lượt 3cm và 4cm.
Hai cung tròn này cắt nhau tại điểm thứ 3.
Nối các điểm ta được tam giác cần dựng.
+ Bộ ba 2cm, 4cm, 5cm (4-2 < 5 < 4+2)
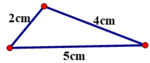
Dựng đoạn thẳng bằng 4cm.
Dựng đoạn thẳng bằng 5cm.
Từ hai đầu đoạn thẳng dựng các cung tròn bán kính lần lượt 2cm và 4cm.
Hai cung tròn này cắt nhau tại điểm thứ 3.
Nối các điểm ta được tam giác cần dựng.
Vậy ta dựng được tất cả 3 tam giác.