Gọi m là số thực để hàm số y= (x+ m)3 đạt giá trị lớn nhất bằng 8 trên đoạn [1; 2]. Khẳng định nào dưới đây đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Xét hàm số ![]() hàm số liên tục trên R
hàm số liên tục trên R
Có ![]()
![]()
![]() đồng biến trên [2;4]
đồng biến trên [2;4]
![]()
Nên ![]()
Do đó ![]()
![]()
Ta có ![]()
![]()
![]()
Dấu bằng xảy ra 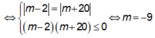
Vậy ![]()
![]()

Chọn A
Kiến thức bổ sung: Dạng toán tìm GTLN, GTNN của hàm số y = |u(x)| trên đoạn [a;b]
Gọi M, m lần lượt là GTLN, GTNN của hàm số u(x) trên đoạn [a;b]
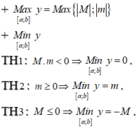
Đặt: ![]()
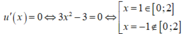
Ta có: ![]()
Suy ra: ![]()
![]()
TH1: ![]()
![]() (loại)
(loại)
(vì ko thỏa mãn giả thiết Aa = 12)
TH2: ![]()
![]()
Từ giả thiết: Aa = 12 ![]()
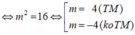
TH3: ![]()
![]()
Từ giả thiết: Aa = 12 ![]()
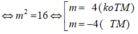
Kết hợp các trường hợp suy ra: S = {-4;4}
Vậy tổng các phần tử của bằng: (-4) + 4 = 0.


Vì hàm số đã cho là hàm bậc nhất trên bậc nhất nên hàm số đơn điệu trên từng khoảng xác định của hàm số.
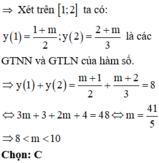

Chọn B
Xét hàm số g(x) = x 3 - 3 x + m trên ℝ
![]()
Bảng biến thiên của hàm số g(x):

Đồ thị của hàm số y = |g(x)| thu được bằng cách giữ nguyên phần đồ thị phía trên trục hoành của (C): y = g(x), còn phần đồ thị phía dưới trục hoành của (C): y = g(x) thì lấy đối xứng qua trục hoành lên trên. Do đó, ta có biện luận sau đây:
Ta xét các trường hợp sau:
![]() Khi đó:
Khi đó: ![]() nên
nên
![]()
![]()
Như vậy ![]() (loại)
(loại)
![]() Khi đó:
Khi đó: ![]() , nên
, nên
![]()
![]()
Như vậy ![]() (thỏa mãn)
(thỏa mãn)
![]() (loại)
(loại)

![]() do đó
do đó![]() (thỏa mãn)
(thỏa mãn)
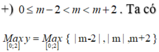
![]() do đó
do đó
![]() (thỏa mãn)
(thỏa mãn)
Suy ra S = {-1;1}. Vậy chọn B
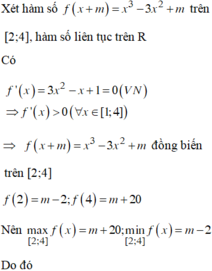
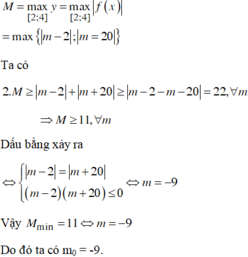
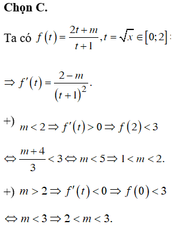

Ta có đạo hàm y’ = 3( x+ m) 2≥0 với mọi x.
=> Hàm số đồng biến trên đoạn [1; 2] nên hàm số đạt GTLN tại x = 2.
Khi đó; y( 2) = 8 khi và chỉ khi : ( 2+m) 3 = 8 hay m= 0
Chọn C.