Tìm x: x - 4 9 = 3 7 : 9 14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
19 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
D
18 tháng 4 2023
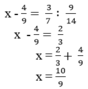
a) x - 3/2 = 4/3
x = 4/3 + 3/2
x = 8/6 + 9/6 = 17/6
b) 2/5 * x = 1/3
x = 1/3 : 2/5
x = 1/3 x 5/2 = 5/6
c) x - 4/9 = 3/7 : 9/14
x - 4/9 = 2/3
x = 2/3 + 4/9
x = 6/9 + 4/9 = 10/9
d) 3/5 * x - 1/2 = 1/5
3/5 * x = 1/5 + 1/2 = 7/10
x = 7/10 : 3/5
x = 7/10 * 5/3 = 7/6
S
18 tháng 4 2023
a/\(x-\dfrac{3}{2}=\dfrac{4}{3}\)
\(x=\dfrac{4}{3}+\dfrac{3}{2}\)
\(x=\dfrac{17}{6}\)
b/\(\dfrac{2}{5}\times x=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}:\dfrac{2}{5}\)
\(x=\dfrac{5}{6}\)
c/\(x-\dfrac{4}{9}=\dfrac{3}{7}:\dfrac{9}{14}\)
\(x-\dfrac{4}{9}=\dfrac{2}{3}\)
\(x=\dfrac{2}{3}+\dfrac{4}{9}\)
\(x=\dfrac{10}{9}\)
d/\(\dfrac{3}{5}\times x-\dfrac{1}{2}=\dfrac{1}{5}\)
\(\dfrac{3}{5}\times x=\dfrac{1}{5}+\dfrac{1}{2}\)
\(\dfrac{3}{5}\times x=\dfrac{7}{10}\)
\(x=\dfrac{7}{10}:\dfrac{3}{5}\)
\(x=\dfrac{7}{6}\)
HM
1
2 tháng 5 2022
\(x:\dfrac{3}{4}\) = \(\dfrac{9}{14}-\dfrac{1}{7}\)
\(x:\dfrac{3}{4}\) = \(\dfrac{1}{2}\)
\(x=\dfrac{1}{2}\) x \(\dfrac{3}{4}\)
\(x=\dfrac{3}{8}\)
\(x\)x \(\dfrac{1}{2}-\dfrac{1}{4}\)=\(\dfrac{2}{3}\)
\(x\) x \(\dfrac{1}{4}\) =\(\dfrac{2}{3}\)
\(x\) = \(\dfrac{2}{3}:\dfrac{1}{4}\)
\(x\) \(\dfrac{8}{3}\)
TL
5
8 tháng 3 2022
b: \(\Leftrightarrow\left(x-\dfrac{1}{2}\right):\dfrac{1}{3}=9+\dfrac{5}{7}-\dfrac{5}{7}=9\)
=>x-1/2=27
hay x=55/2
c: =>1/2x-3/4=42/63=2/3
=>1/2x=17/12
hay x=17/6
26 tháng 8 2023
Bài 1:
a) \(x.\dfrac{3}{4}=\dfrac{9}{14}\)
\(\Rightarrow x=\dfrac{9}{14}:\dfrac{3}{4}\)
\(\Rightarrow x=\dfrac{6}{7}\)
b) \(x:\dfrac{5}{9}=\dfrac{3}{10}\)
\(\Rightarrow x=\dfrac{3}{10}.\dfrac{5}{9}\)
\(\Rightarrow x=\dfrac{1}{6}\)
AD
18 tháng 3 2021
a)\(x+\frac{15}{16}+\frac{7}{8}=\frac{15}{4}\)
\(x+\frac{29}{16}=\frac{15}{4}\)
\(x=\frac{15}{4}-\frac{29}{16}\)
\(x=\frac{31}{16}\)
b)\(x-\frac{27}{28}-\frac{9}{14}=\frac{13}{7}\)
\(x-\frac{45}{28}=\frac{13}{7}\)
\(x=\frac{13}{7}+\frac{45}{28}\)
\(x=\frac{97}{28}\)
c)\(x\times\frac{1}{5}+x+\frac{1}{6}=\frac{2}{3}\)
\(x\times\frac{1}{5}+x=\frac{2}{3}-\frac{1}{6}\)
\(x\times\left(\frac{1}{5}+1\right)=\frac{1}{2}\)
\(x\times\frac{6}{5}=\frac{1}{2}\)
\(x=\frac{1}{2}:\frac{6}{5}\)
\(x=\frac{5}{12}\)
d)\(x:14=\frac{1}{4}+\frac{2}{9}+\frac{3}{4}\)
\(x:14=\frac{11}{9}\)
\(x=\frac{11}{9}\times14\)
\(x=\frac{154}{9}\)
#H
HK
2
C
20 tháng 3 2023
`x xx 6/7=5/14`
`=>x=5/14:6/7`
`=>x=5/14xx7/6`
`=>x=35/84`
`=>x=5/12`
Vậy `x=5/12`
__
`x:2/3=4/9`
`=>x=4/9xx2/3`
`=>x=8/27`
Vậy `x=8/27`
__
`x-1/4=3/2`
`=>x=3/2+1/4`
`=>x=6/4+1/4`
`=>x=7/4`
Vậy `x=7/4`
__
`x+4/5=8/9`
`=>x=8/9-4/5`
`=>x=40/45-36/45`
`=>x=4/45`
Vậy `x=4/45`
T
20 tháng 3 2023
\(x\cdot\dfrac{6}{7}=\dfrac{5}{14}\)
\(x\) \(=\dfrac{5}{14}:\dfrac{6}{7}\)
\(x\) \(=\dfrac{5}{12}\)
\(x:\dfrac{2}{3}=\dfrac{4}{9}\)
\(x\) \(=\dfrac{4}{9}\cdot\dfrac{2}{3}\)
\(x\) \(=\dfrac{8}{27}\)
\(x-\dfrac{1}{4}=\dfrac{3}{2}\)
\(x\) \(=\dfrac{3}{2}+\dfrac{1}{4}\)
\(x\) \(=\dfrac{7}{4}\)
\(x+\dfrac{4}{5}=\dfrac{8}{9}\)
\(x\) \(=\dfrac{8}{9}-\dfrac{4}{5}\)
\(x\) \(=\dfrac{4}{45}\)
9 tháng 3 2022
a: \(\dfrac{-8}{3}\cdot\dfrac{15}{24}=\dfrac{-8}{24}\cdot\dfrac{15}{3}=\dfrac{-1}{3}\cdot5=-\dfrac{5}{3}\)
b: \(=\dfrac{3}{4}\cdot\dfrac{1}{-9}=\dfrac{-1}{12}\)
c: \(x=-\dfrac{7}{6}+\dfrac{5}{8}=-\dfrac{13}{24}\)
d: \(x=-\dfrac{14}{25}-\dfrac{3}{4}=\dfrac{-56-75}{100}=\dfrac{-131}{100}\)
18 tháng 1 2024
b: \(\dfrac{5}{7}-\dfrac{2}{3}\cdot x=\dfrac{4}{5}\)
=>\(\dfrac{2}{3}x=\dfrac{5}{7}-\dfrac{4}{5}=\dfrac{25-28}{35}=\dfrac{-3}{35}\)
=>\(x=-\dfrac{3}{35}:\dfrac{2}{3}=\dfrac{-3}{35}\cdot\dfrac{3}{2}=-\dfrac{9}{70}\)
c: \(\dfrac{1}{2}x+\dfrac{3}{5}x=-\dfrac{2}{3}\)
=>\(x\left(\dfrac{1}{2}+\dfrac{3}{5}\right)=-\dfrac{2}{3}\)
=>\(x\cdot\dfrac{5+6}{10}=\dfrac{-2}{3}\)
=>\(x\cdot\dfrac{11}{10}=-\dfrac{2}{3}\)
=>\(x=-\dfrac{2}{3}:\dfrac{11}{10}=-\dfrac{2}{3}\cdot\dfrac{10}{11}=\dfrac{-20}{33}\)
d: \(\dfrac{4}{7}\cdot x-x=-\dfrac{9}{14}\)
=>\(\dfrac{-3}{7}\cdot x=\dfrac{-9}{14}\)
=>\(\dfrac{3}{7}\cdot x=\dfrac{9}{14}\)
=>\(x=\dfrac{9}{14}:\dfrac{3}{7}=\dfrac{9}{14}\cdot\dfrac{7}{3}=\dfrac{3}{2}\)
VN
Võ Ngọc Phương
VIP
16 tháng 3 2023
x - \(\dfrac{3}{7}:\dfrac{9}{14}=\dfrac{-7}{3}\)
x - \(\dfrac{3}{7}\) = \(\dfrac{-7}{3}x\dfrac{9}{14}\)
x - \(\dfrac{3}{7}\) = \(\dfrac{-63}{42}\)
x = \(\dfrac{-63}{42}+\dfrac{3}{7}\)
x = \(\dfrac{-63}{42}+\dfrac{18}{42}\)
x = \(\dfrac{45}{42}\) = \(\dfrac{15}{14}\)