Tính nhanh b.256x236+256x256-256
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 2 2018
Đúng(0)
Những câu hỏi liên quan
TT
3
MC
14 tháng 7 2021
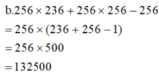
\(\frac{64\times64+256\times256}{256\times256+1024\times1024}=\frac{64^2}{1024\times1024}=\frac{64^2}{16^2\times64^2}=\frac{1}{16^2}=\frac{1}{256}\)
9 tháng 1 2018
\(\frac{64x64+256x256}{256x256+1024x1024}\)
= \(\frac{64x64}{1024x1024}\)
= \(\frac{64x64}{64x16x64x16}\)
= \(\frac{1}{256}\)
TM
2
20 tháng 1 2018
A=[(-125).12].(-18)
A= (-1500) .(-18)
Vậy A= 27000
B= (-256).43+(-256).25-256.32
B=(-256).(43+25+32)
B=(-256).100
Vậy B=-25600
C=1-2+3-4+...+999-1000
C=(1-2)+(3-4)+.....+(999-1000)
C=(-1)+(-1)+...+(-1)
Nhận xét: vì mỗi số hạng trong C cách nhau 1 đơn vị.
=> C có số hạng là: (1000-1):1+1=1000
C có số cặp là: 1000:2=500
=>C=500.(-1)
Vậy C= -500
HT
2
20 tháng 4 2022
\(54\times113+45\times113+113=\left(54+45+1\right)\times113=100\times113=11300\)
\(256\times236+256\times256-256=\left(236+256-1\right)\times256=419\times256=125696\)
PT
1
N
5
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
25 tháng 11 2023
128 x 68 + 16 x 256
= 128 x 68 + 16 x 2 x 128
= 128 x 68 + 32 x 128
= 128 x (68+32)
= 128 x 100 = 12 800
DH
4
1 tháng 8 2017
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{256}\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{128}\)
\(2A-A=\left(1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{128}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{256}\right)\)
\(A=1-\frac{1}{256}=\frac{255}{256}\)
\(B=\frac{5}{1.2}+\frac{5}{3.4}+...+\frac{5}{91.92}\)
\(B=5.\left(\frac{1}{1.2}+\frac{1}{3.4}+...+\frac{1}{91.92}\right)\)
\(B=5.\left(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{91}-\frac{1}{92}\right)\)
\(B=5.\left(\frac{1}{47}+\frac{1}{48}+...+\frac{1}{92}\right)\)