Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1, AC=2, B A C ^ = 120 ° . Giả sử D là trung điểm của cạnh CC’ và B D A ^ = 90 ° . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 15 2
B. V = 3 15
C. V = 3 15 7
D. V = 2 15
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Phương pháp tọa độ hóa.
Cách giải:
Cách 1:
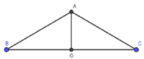
Gọi O là trung điểm của BC.
Tam giác ABC là tam giác cân, AB = AC = a, B A C ^ = 120 0
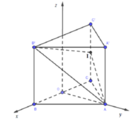
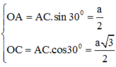
Ta gắn hệ trục tọa độ như hình bên:
Trong đó, O(0;0;0); A(0; a 2 ;0); B' ( a 3 2 ;0;a); I( - a 3 2 ;0; a 2 )
Mặt phẳng (ABC) trùng với mặt phẳng (Oxy) và có VTPT là n 1 → = ( 0 ; 0 ; 1 )
I B ' → = a 3 ; 0 ; a 2 ; I A → = a 3 2 ; a 2 ; - a 2
Mặt phẳng (IB’A) có 1 VTPT n 2 → = 2 3 ; 0 ; 1 ; 3 ; 1 ; - 1 = 1 ; 3 3 ; 2 3
Côsin góc giữa hai mặt phẳng (ABC) và (IB’A) :
cos((ABC);(AB'I)) = |cos(
n
1
→
;
n
2
→
)| = 
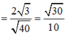
Cách 2:
Trong (ACC’A’) kéo dài AI cắt AC’tại D.
Trong (A’B’C’) kẻ A’H ⊥ B’D ta có:
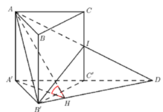
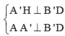
![]()
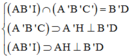
=> ![]()
Ta dễ dàng chứng minh được C’ là trung điểm của AD’
![]()
![]()
=> 
Xét tam giác A’B’D có
B'D = ![]()
![]()
=> 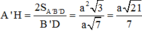
Xét tam giác vuông AA'H có :
![]()
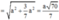
=> 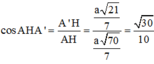

\(2x\left(y-x\right)=a^2>0\Rightarrow y>x\)
Qua \(B_1\) kẻ đường thẳng song song BC cắt \(CC'\) tại D \(\Rightarrow DC_1=y-x\) và \(B_1D=BC=a\)
Áp dụng Pitago ta có:
\(AC_1^2=AC^2+AC_1^2=a^2+y^2\)
\(AB_1^2=AB^2+BB_1^2=a^2+x^2\)
\(B_1C_1^2=B_1D^2+DC_1^2=a^2+\left(y-x\right)^2\)
\(\Rightarrow AB_1^2+B_1C_1^2=2a^2+x^2+\left(y-x\right)^2=2a^2+2x^2+y^2-2xy\)
\(=2a^2+2x^2+y^2-\left(2x^2+a^2\right)=a^2+y^2=AC_1^2\)
\(\Rightarrow\Delta AB_1C_1\) vuông tại \(B_1\) theo Pitago đảo.
b.
Do \(B_1\) là trung điểm BB' \(\Rightarrow x=\dfrac{BB'}{2}\), mà \(y=2x\Rightarrow y=BB'\Rightarrow C_1\) trùng C'
Do \(CC',B_1B\) vuông góc mặt đáy \(\Rightarrow\) tam giác ABC là hình chiếu vuông góc của tam giác \(AB_1C_1\) lên (ABC)
Theo công thức diện tích hình chiếu:
\(S_{ABC}=S_{AB_1C_1}.cos\alpha\Rightarrow S_{AB_1C_1}=\dfrac{S_{ABC}}{cos\alpha}=\dfrac{a^2\sqrt{3}}{4cos\alpha}\)
Gọi D là trung điểm AC' (hay \(AC_1\)) và E là trung điểm AC
\(\Rightarrow\) \(BEDB_1\) là hình chữ nhật \(\Rightarrow B_1D=BE=\dfrac{a\sqrt{3}}{2}\)
\(B_1C'=B_1A=\sqrt{a^2+\left(\dfrac{x}{2}\right)^2}\) nên tam giác \(AB_1C'\) cân tại \(B_1\Rightarrow B_1D\) đồng thời là đường cao
\(\Rightarrow S_{AB_1C_1}=\dfrac{1}{2}B_1D.AC'=\dfrac{a^2\sqrt{3}}{4cos\alpha}\Rightarrow AC'=\dfrac{a^2\sqrt{3}}{2cos\alpha.B_1D}=\dfrac{a}{cos\alpha}\)
\(\Rightarrow AA'=\sqrt{AC'^2-AC^2}=\sqrt{\dfrac{a^2}{cos^2\alpha}-a^2}=a.tan\alpha\)