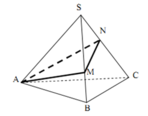
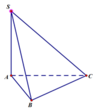
Cho hình chóp tam giác đều S.ABC có SA=a , A S B ⏞ = 30 ° Người ta muốn trang trí cho hình chóp bằng một dây đèn nháy chạy theo các điểm A, M, N rồi quay lại A (đúng một vòng) như hình bên dưới. Độ dài ngắn nhất của dây đèn nháy là:
A. a 2 2
B. a 2
C. a 3
D. a 3 3


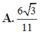
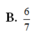
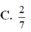
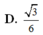

Đáp án B
Trải hình ra ta thu được:
Dễ thấy AM + MN + NA đạt giá trị nhỏ nhất khi A, M, N, A thẳng hàng
Lại có S.ABC là hình chóp tam giác đều
ð ∆SAB = ∆SBC = ∆SAC (c.c.c)
⇒ AS B ^ = B S C ^ = C S A ^ ⇒ AS A ^ = 90 °
AM + MN + N A m i n = a 2