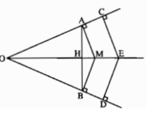
Cho góc đỉnh O khác góc bẹt. Từ một điểm M trên tia phân giác của góc O, kẻ các đường vuông góc MA, MB đến hai cạnh của góc này. Chứng minh rằng AB ⊥ OM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2018
Giải
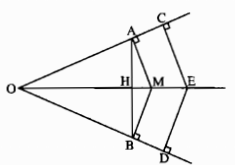
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.
LP
8 tháng 4 2022
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.
2 tháng 3 2022
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
hayΔMBA cân tại M
b: Ta có: ΔOAM=ΔOBM
nên OA=OB
=>ΔOAB cân tại O
mà OM là đường phân giác
nên OM là đường cao
CM
27 tháng 7 2018
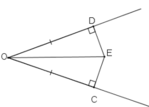
Xét ΔODE và ΔOCE vuông tại D và C có:
OE chung
OD = OC (gt)
⇒ ΔODE = ΔOCE ( cạnh huyền- cạnh góc vuông)
⇒ ∠DOE = ∠COE
⇒ OE là phân giác của góc O
TN
25 tháng 8 2016
Xét tam giác OBM vuông tại B và tam giác OAM vuông tại A ta có
OM=OM (cạnh chung)
góc BOM = góc AOM ( OM là tia phân giác góc AOB)
-> tam giác OBM = tam giac OAM (ch-gn)
-> OB = OA ( 2 cạnh tương ứng)
Gọi I là giao điềm OM và AB
xét tam giác OBI và tam giác AOI ta có
OB=OA (cmt)
OI=OI ( cạnh chung)
goc BOI=goc AOI ( OI là tia phân giác góc BOI)
-> tam giac OBI=tam giac OAI ( c-g-c)
-> goc BIO= goc AIO (2 góc tương ứng)
mà góc BIO+ góc AIO =180 (2 góc kề bù)
nên góc BIO+ góc BIO=180
-> 2 góc BIO=180
góc BIO=180/2=90
-> AB vuong goc OM tại I
25 tháng 8 2016
Đồng ý với Thao Nhi.
Thêm cách nầy của mình có đc ko nhé
Tam giác BOI = Tam giắc AOI => OB=OA nên tam giác AOB cân tại O => OI Là phân giác và là đường cao => OI Vuông góc với AB
CM
1 tháng 1 2019
1) Hình vẽ câu 1) đúng
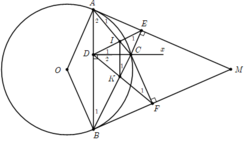
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B
LD
31 tháng 3 2021
a) Xét\(\Delta OAM\)và \(\Delta OAN\)có:
\(\hept{\begin{cases}OA:chung\\gócAOM=gócAON\\gócOAM=gócOAN\left(=90^0\right)\end{cases}}\)
\(\Rightarrow\Delta OAM=\Delta OAN\left(ch-gn\right)\)
\(\Rightarrow OM=ON\left(đpcm\right)\)
b) Xét \(\Delta OEM\)và \(\Delta OEN\)có:
\(\hept{\begin{cases}OE:chung\\gócMOE=gócNOE\\OM=ON\end{cases}}\)
\(\Rightarrow\Delta OEM=\Delta OEN\left(c.g.c\right)\)
\(\Rightarrow gócOEM=gócOEN\left(đpcm\right)\)
Gọi H là giao điểm của AB và OM.
Xét ΔAOM (vuông tại A) và ΔBOM (vuông tại B) có:
OM chung
∠MOA = ∠MOB ( vì OM là tia phân giác của góc xOy)
⇒ ΔAOM = ΔBOM (cạnh huyền – góc nhọn)
⇒ OA = OB.
+) Xét ΔOAH và ΔBOH có:
OA = OB ( chứng minh trên )
OH chung
∠AOH = ∠BOH ( vì OH là tia phân giác của góc xOy)
⇒ ΔOAH = ΔOBH (c.g.c)
⇒ ∠OHA = ∠OHB. Mà ∠OHA + ∠OHB = 180o ( hai góc kề bù)
⇒ ∠OHA = ∠OHB = 90o
Vậy AB ⊥ OM.