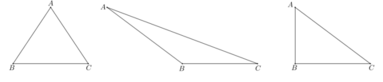
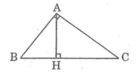
Vẽ đường cao AH của tam giác ABC trong mỗi trường hợp sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn:
- Đặt một cạnh góc vuông của ê-ke trùng với đường thẳng BC
- Trượt ê-ke theo đường thẳng để cạnh góc vuông còn lại của ê-ke gặp điểm A, vạch đường cao AH theo cạnh đó…

- Đặt một cạnh góc vuông của ê-ke trùng với đường thẳng BC
- Trượt ê-ke theo đường thẳng để cạnh góc vuông còn lại của ê-ke gặp điểm A, vạch đường cao AH theo cạnh đó…

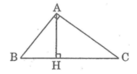
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH = 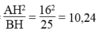
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = ![]()
≈ 29,68
A C 2 = H C . B C
⇒ AC = ![]() ≈ 18,99
≈ 18,99

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ BC = ![]() = 24
= 24
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
A
C
2
=
H
C
.
B
C
⇒ AC = ![]() ≈ 20,78
≈ 20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
A
H
2
=
H
B
.
B
C
⇒ AH = ![]()

a. - Áp dụng hệ thức về cạnh và đường cao trong Δ vuông vào ΔABC vuông tại A ta có :
\(AH=\sqrt{CH.BH}=\sqrt{2.4}=2\sqrt{2}\) ( Đ.lý 2 )
- Áp dụng đ.lý Pytago vào \(\Delta AHB\perp H\) ta có :
\(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{2}\right)^2+4^2}=2\sqrt{6}\)
- \(BC=2+4=6\)
- Theo đ.lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}\)
b. - Áp dụng hệ thức...trong Δ vuông ABC ta có :
+ \(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=24\) ( Đ.lý 1 )
\(\Rightarrow CH=BC-BH=24-6=18\)
+ \(AH=\sqrt{BH.CH}=\sqrt{6.18}=6\sqrt{3}\) ( Đ.'ý 2 )
- Theo đ.lý Pytago ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{24^2-12^2}=12\sqrt{3}\)
a, BC = BH+HC
*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)
*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)
*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)
b,Theo định lý pytago ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)
*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)
*\(CH=BC-BH=24-6=18\)
\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)

Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=13^2-5^2=144\)
hay AH=12(cm)
Xét ΔABH vuông tại H có
\(\sin\widehat{B}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\Leftrightarrow\cos\widehat{C}=\dfrac{12}{13}\)
hay \(\sin\widehat{C}=\dfrac{5}{13}\)
Hướng dẫn giải: