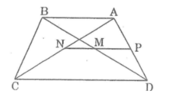
Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng: MN // AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2018
Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2
VS
19 tháng 3 2020
a. Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có: 
Suy ra: 
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong ΔACD, ta có 
Suy ra: 
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
b. Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2
16 tháng 2 2020
a, kẻ AM cắt CD tại E
xét tam giác AMB và tam giác EMD có : góc AMB = góc EMD (đối đỉnh)
DM = MB do M là trung điểm của BD (gt)
góc ABM = góc MDE (so le trong AB // DC)
=> tam giác AMB = tam giác EMD (g-c-g) (1)
=> AM = ME (đn) có M nằm giữa A và E
=> M là trung điểm của AE
N là trugn điểm của AC (gt) ; xét tam giác AEC
=> MN là đường trung bình của tam giác AEC (đn) (2)
=> MN // EC (Đl)
CE // AB
=> MN // AB
b, (2) => MN = EC/2
EC = CD - DE
=> MN = (CD - DE) : 2
(1) => DE = AB
=> MN = (CD - AB) : 2
2 tháng 2 2023
a: Gọi F là trung điểm của BC
Xét ΔCAB có
N,F lần lượt là trung điểm của CA,CB
nên NFlà đường trung bình
=>NF//AB và NF=AB/2
Xét ΔDCB có
M,F lần lượt là trung điểm của BD,BC
nên MF là đường trung bình
=>MF//CD và MF=CD/2
=>MF//AB
mà NF//AB
nên M,N,F thẳng hàng
=>MN//AB
b: MN=MF-FN=1/2(CD-AB)
26 tháng 2 2017
Trước tiên kẻ AM cắt CD tại I
Ta xét tam giác AMB và IMD
Hai tam giác đó bằng nhau vì MB=MD (gt) và góc AMB=IMD (đđ) và góc ABM=IDM (so le trong vì AB//CD)
Vì vậy mà AB=ID và MA=MI
Xét tam giác AIC có MA=MI và NA=NC nên MN là đường trung bình của tam giác AIC nên MN//CI và MN=(1/2)CI
Do CI=CD-ID cũng như CI=CD-AB (do AB=ID cmt) và MN=(1/2)CI
nên MN=(1/2)(CD-AB)
CM
25 tháng 1 2018
Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC
MN
29 tháng 2 2020
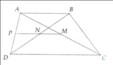
Kẻ AN cắt CD tại E
Xét △ANB và △END có :
^ANB = ^END (đối đỉnh)
NB = ND (gt)
^ABD = ^BDE (so le trong)
\(\Rightarrow\)△ANB = △END (g.c.g)
\(\Rightarrow\)AN = NE (cặp cạnh tương ứng)
Xét △AEC có : AM = MC
AN = NE
\(\Rightarrow\)MN // EC
\(\Rightarrow\)MN // AB // CD (ĐPCM)
12 tháng 5 2017
Lời giải
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???
Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có: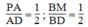
Suy ra: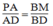
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong △ ACD, ta có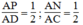
Suy ra: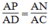
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.