Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
K
Khách
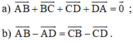
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 7 2018
mik ko bít
I don't now
................................
.............
9 tháng 10 2021
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
ta có: BC=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra BD là đường trung trực của AC
hay A và C đối xứng nhau qua BD
27 tháng 7 2020
Tứ giác ABCD.
Giả sử các góc của tứ giác trên đều nhọn .
Khi đó: \(\widehat{A}< 90^o;\widehat{B}< 90^o;\widehat{C}< 90^o;\widehat{D}< 90^o\)
\(\Leftrightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}< 4\times90^o=360^o\)
Mà tổng các góc trong một tam giác luôn bằng 360 độ
=> Vô Lí
=> Trong một tứ giác bất kì có ít nhất một góc không nhọn.
12 tháng 11 2021
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
a) Ta có:
b) Áp dụng quy tắc trừ hai vec tơ ta có: