Cho 0 ο < α < 90 ο
Chứng minh rằng sinα + cosα > 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C c b a
Xét tam giác vuông có ba cạnh AB, AC , BC lần lượt là c,b,a
a) Ta có : \(tan\alpha=\frac{b}{c}=\frac{\frac{b}{a}}{\frac{c}{a}}=\frac{sin\alpha}{cos\alpha}\)
\(cotg\alpha=\frac{c}{b}=\frac{\frac{c}{a}}{\frac{b}{a}}=\frac{cos\alpha}{sin\alpha}\)
\(tan\alpha.cotg\alpha=\frac{b}{c}.\frac{c}{b}=1\)
b) Ta có : \(sin^2\alpha=\frac{b^2}{a^2},cos^2\alpha=\frac{c^2}{a^2}\Rightarrow sin^2\alpha+cos^2\alpha=\frac{b^2+c^2}{a^2}=\frac{a^2}{a^2}=1\)

a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)

Chọn A.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay 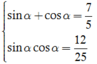 vào P ta được
vào P ta được 

Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do ![]() suy ra sinα < cosα nên sinα - cosα < 0.
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy 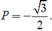
Ta có sinα + cosα > 0 và sinαcosα > 0. Do đó
( sin α + cos α ) 2 = sin 2 α + cos 2 α + 2 sin α cos α
= 1 + 2sinαcosα > 1
Từ đó suy ra: sinα + cosα > 1