Hai con lắc đơn có chiều dài lần lượt là l 1 , l 2 và có chu kì lần lượt là T 1 , T 2 tại một nơi có gia tốc rơi tự do là 9,8 m/ s 2 . Cho biết cũng tại nơi đó, con lắc đơn có chiều dài l 1 + l 2 có chu kì dao động là 2,4 s và con lắc đơn có chiều dài l 1 - l 2 có chu kì dao động là 0,8 s. Hãy tính T 1 , T 2 , l 1 , l 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mk nghĩ làm bài này như sau:
Ta có:\(\begin{cases}T1=2\pi\sqrt{\frac{l1}{g}}\\T2=2\pi\sqrt{\frac{l2}{g}}\end{cases}\)\(\Rightarrow\sqrt{\frac{l1.l2}{g^2}}=\frac{T1.T2}{\left(2\pi\right)^2}\)\(\Rightarrow\frac{1}{\sqrt{g}}.\sqrt{\frac{l1.l2}{g}}=\frac{T1.T2}{\left(2\pi\right)^2}\)
\(\Rightarrow\) \(T3=2\pi\sqrt{\frac{l1.l2}{g}}=\frac{\sqrt{g}}{2\pi}T1.T2\)
Chọn C

[Vật lí 12] con lắc đơn | Cộng đồng học sinh Việt Nam
Ta có biểu thức của các chu kì :
\(T_1=2\pi\sqrt{\frac{l_1}{g}};T_2=2\pi\sqrt{\frac{l_2}{g}};T=2\pi\sqrt{\frac{l_1+l_2}{g}};T'=\sqrt{\frac{l_1-l_2}{g}}\)
\(\Rightarrow\frac{l_1}{T_1^2}=\frac{l_2}{T_2^2}=\frac{l_1+l_2}{T^2}=\frac{l_1-l_2}{T'^2}\)
Vậy \(T_1^2+T_2^2=T^2\) và \(T_1^2-T_2^2=T'^2\)
Do đó : \(T_1=\sqrt{\frac{T^2+T'^2}{2}}=\sqrt{\frac{2,7^2+0,9^2}{2}}\approx2,0\left(s\right)\)
\(T_2=\sqrt{\frac{T^2-T'^2}{2}}=\sqrt{\frac{2,7^2-0,9^2}{2}}\approx1,8\left(s\right)\)
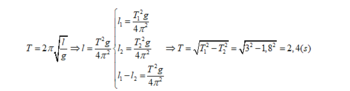

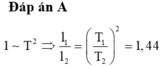
Theo công thức tính chu kỳ ta có
⇒ T 1 = 0,18s; T 2 = 0,16s