Cho tam giác ABC có B ^ = 60 0 , C ^ = 50 0 và AC = 35 cm. Tính diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
22 tháng 7 2015
trên hình kẻ đường cao AH
ta có \(\text{cos 50}=\frac{HC}{AC}\Rightarrow HC=AC.\text{cos 50 }=35.\text{cos 50}\approx22\text{ (cm)}\)
\(\text{sin 50}=\frac{AH}{AC}\Rightarrow AH=AC.\text{sin 50}=35.\text{sin 50}\approx27\left(cm\right)\)
\(\text{tan 60}=\frac{AH}{BH}\Rightarrow BH=\frac{AH}{\text{tan 60}}=\frac{27}{\text{tan 60}}\approx16\left(cm\right)\)
\(\Rightarrow BC=22+16=38\left(cm\right)\)
\(\text{sin 60}=\frac{AH}{AB}\Rightarrow AB=\frac{AH}{\text{sin 60}}=\frac{27}{\text{sin 60}}\approx31\left(cm\right)\)
Diện tích tam giác ABC là:
35+38+31=104 (cm)
VB
0
16 tháng 8 2016
Từ A kẻ đường cao AH vuông góc với BC , từ B kẻ đường cao BK vuông góc với AC
=> AH = sinC x AC = sin 500 x 35 = a
Ta có : AB = \(\frac{AH}{sinB}=\frac{a}{sinB}=b\)
BK = \(sinA\times AB=sin\left(180^o-60^o-50^o\right)=sin70^o\times b\)= c
=> S . ABC = 1/2AC x BK = 1/2 x 35 x c =..........
a,b,c mình đặt thay cho độ dài AH , AB, BK
17 tháng 8 2016
Sao bạn không tính hẳn AH, AB, BK mà phải kí hiệu a, b,c vậy?
NH
1
NV
15 tháng 8 2016
Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
\(cosC=\frac{HC}{AC}\Rightarrow HC=cosC.AC=cos50.35\approx22cm\)
\(\Rightarrow AH=\sqrt{AC^2-HC^2}=\sqrt{35^2-22^2}=\sqrt{741}cm\)
Trong tam giác vuông AHB ta có:
\(sinB=\frac{AH}{AB}\Rightarrow AB=\frac{AH}{sinB}=\frac{\sqrt{741}}{sin60}=2\sqrt{247}cm\)
\(\Rightarrow HB=\sqrt{AB^2-AH^2}=\sqrt{\left(2\sqrt{247}\right)^2-741}=\sqrt{247}cm\)
Vậy \(S_{ABC}=\frac{AH\left(HB+HC\right)}{2}=\frac{\sqrt{741}.\left(\sqrt{247}+22\right)}{2}\approx513cm\)
CT
0
LD
20 tháng 2 2018
Bài 2.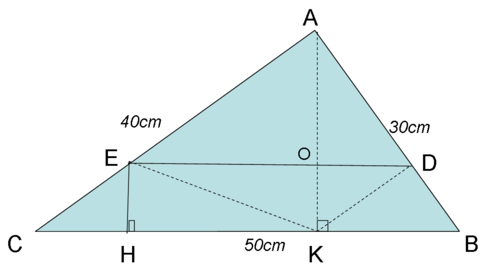 
a) Trong tam giác vuông thì 2 cạnh góc vuông cũng chính là 2 đường cao của tam giác đó.
Vậy đường cao AB = 30 cm ; đường cao AC = 40 cm
Đường cao tam giác ABC còn lại đỉnh A là : 30 x 40 : 50 = 24 (cm)
b) S_ECK + S_DKB = CK x 6 : 2 + KB x 6 : 2 = (CK+KB) x 6 : 2 = 50 x 3 = 150 (cm2)
S_AEKD = 30 x 40 : 2 - 150 = 450 (cm2)
Xét tam giác AED và EDK chung đáy ED chiều cao AO = 24 - 6 = 18 (cm)
Tỉ lệ AO/OK = 18/6 = 3. Vậy S_AED = 3 x S_EDK
Diện tích tam giác AED là : 450 : (1+3) x 3 = 337,5 (cm2)
27 tháng 1 2023
a: ΔABC cân tại A
mà AM là phân giác
nên AM vuôg góc BC và M là trung điểm của BC
\(BM=CM=\dfrac{60}{2}=30\left(cm\right)\)
\(AM=\sqrt{50^2-30^2}=40\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot40\cdot60=20\cdot60=1200\left(cm^2\right)\)
b: Xét ΔOAK và ΔOCM có
OA=OC
góc AOK=góc COM
OK=OM
=>ΔOAK=ΔOCM
=>góc OAK=góc OCM
=>AK//CM
b: Xét tứ giác AMCK có
AK//CM
AK=CM
góc AMC=90 độ
=>AMCK là hfinh chữ nhật
d: Để AMCK là hình vuông thì AM=CM=BC/2
=>ΔABC vuông tại A
S A B C = 509 , 08 c m 2