Rút gọn các biểu thức sau (với a và b không âm):
√(3a3 ) . √12a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 10 2017
a ) √ ( 3 a 3 ) . √ 12 a = √ ( 3 a 3 . 12 a ) = √ ( 36 a 4 ) = √ ( ( 6 a 2 ) 2 ) = 6 a 2 ( d o a 2 ≥ 0 ) b ) √ ( 2 a . 32 a b 2 ) = √ ( 64 2 b 2 ) = √ ( ( 8 a b ) 2 ) = 8 a b ( d o a ≥ 0 ; b ≥ 0 )
6 tháng 9 2016
a) \(\sqrt{3a^3}\cdot\sqrt{12a}=\sqrt{3a^3\cdot12a}=\sqrt{36a^4}=6a^2\)
b) \(\sqrt{2a\cdot32ab^2}=\sqrt{64a^2b^2}=8ab\)
PT
1
CM
3 tháng 4 2019
5√4a6 - 3a3 = 5√(2a3)2 - 3a3
= 5|2a3| - 3a3
Với a < 0 thì |2a3| = – 2a3 nên
5|2a3| - 3a3 = -10a3 - 3a3 = -13a3
PT
1
CM
6 tháng 12 2018
√(2a . 32ab2) = √(64a2b2 )
= √((8ab)2) = 8ab (do a ≥ 0; b ≥ 0)
CM
17 tháng 11 2019
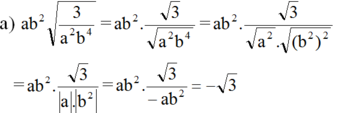
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
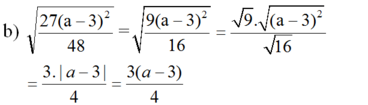
(vì a > 3 nên |a - 3| = a - 3)
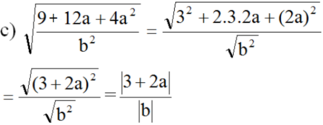
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
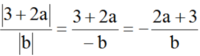
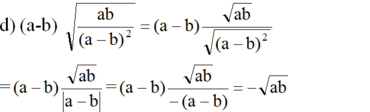
(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)
CM
6 tháng 10 2017
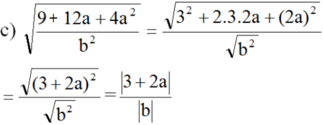
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
CM
29 tháng 3 2019
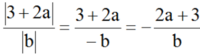
Biến đổi được: x = 2 ( a + b ) 3 ( a 3 − b 3 ) ; y = 9 ( a − b ) 2 4 ( a + b )
⇒ P = x . y = 2 ( a + b ) 3 ( a 3 − b 3 ) . 9 ( a − b ) 2 4 ( a + b ) = 3 ( a − b ) 2 ( a 2 + ab + b 2 )
CM
22 tháng 1 2017
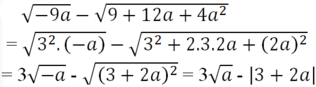
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
√(3a3 ).√12a = √(3a3.12a) = √(36a4 )
= √((6a2 )2 ) = 6a2 (do a2 ≥ 0)