Giai đoạn 1 của sản xuất công nghiệp tác động vào đối tượn tạo ra
A. máy móc
B. nguyên liệu
C. tư liệu sản xuất
D. vật phẩm tiêu dùng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
26 tháng 12 2023
a) Gang và thép thuộc nhóm vật liệu kim loại.
b) Gang và thép được sản xuất chủ yếu từ quặng sắt, một khoáng sản chứa oxit sắt. Quá trình sản xuất bao gồm việc chiết tách sắt từ quặng, sau đó chế biến và hợp kim để tạo ra sản phẩm cuối cùng.
c) Tác hại đối với môi trường khi khai thác nguồn nguyên liệu sắt có thể bao gồm:
-
Khai thác mỏ: Việc khai thác quặng sắt có thể gây ra đất đai và động lực học của vùng mỏ bị tác động nặng nề. Nó cũng có thể dẫn đến sự mất mát đa dạng sinh học và môi trường sống tự nhiên.
-
Sử dụng năng lượng: Quá trình sản xuất gang và thép đòi hỏi lượng lớn năng lượng. Sử dụng năng lượng từ nguồn hóa thạch có thể tạo ra khí nhà kính và góp phần vào biến đổi khí hậu.
-
Xử lý chất thải: Việc xử lý chất thải từ quá trình sản xuất kim loại có thể tạo ra chất thải và khó khăn trong việc xử lý chúng một cách an toàn và hiệu quả.
Để giảm tác động của ngành công nghiệp gang và thép lên môi trường, các quá trình sản xuất và xử lý đã được phát triển để tối ưu hóa sự sử dụng nguyên liệu, giảm lượng chất thải, và sử dụng nguồn năng lượng tái tạo. Các biện pháp bảo vệ môi trường, như tái chế và sử dụng kim loại tái chế, cũng giúp giảm áp lực lên nguồn nguyên liệu tự nhiên.
25 tháng 9 2023
Tham khảo:
Gọi x, y lần lượt là số kilogam sản phẩm loại A, loại B mà công ty đó sản xuất.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Nguyên liệu loại I có số kilogam dự trữ là 8 kg nên \(2x + y \le 8\)
- Nguyên liệu loại II có số kilogam dự trữ là 24 kg nên \(4x + 4y \le 24\)
- Nguyên liệu loại III có số kilogam dự trữ là 8 kg nên \(x + 2y \le 8\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}2x + y \le 8\\4x + 4y \le 24\\x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
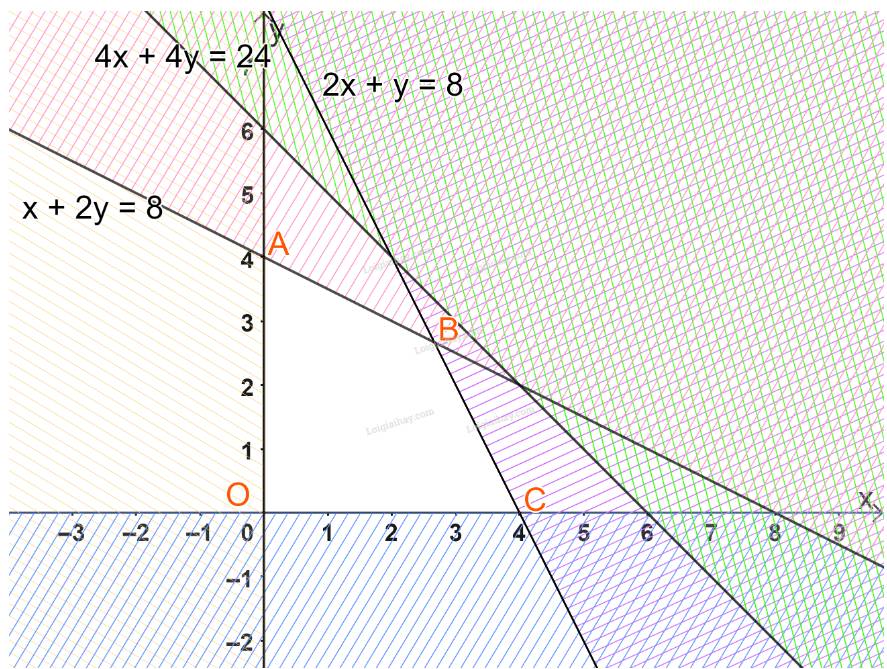
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(0;4),\)\(B(\frac{8}{3};\frac{8}{3}),\)\(C(4;0).\)
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu về, ta có: \(F = 30x + 50y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 30.0 + 50.0 = 0\)
Tại \(A(0;4),\)\(F = 30.0 + 50.4 = 200\)
Tại \(B(\frac{8}{3};\frac{8}{3}),\)\(F = 30.\frac{8}{3} + 50.\frac{8}{3} = \frac{{640}}{3}\)
Tại \(C(4;0):\)\(F = 30.4 + 50.0 = 120\)
F đạt giá trị lớn nhất bằng \(\frac{{640}}{3}\) tại \(B(\frac{8}{3};\frac{8}{3}).\)
Vậy công ty đó nên sản xuất \(\frac{8}{3}kg\) sản phẩm mỗi loại để tiền lãi thu về lớn nhất.
Đáp án B