Cho hình vẽ bên, biết a//ba//ba//b, ˆBCD=120∘ˆBCD=120∘BCD^=120∘. Số đo...
Đọc tiếp
Cho hình vẽ bên, biết a//ba//ba//b, ˆBCD=120∘ˆBCD=120∘BCD^=120∘. Số đo góc ˆADCˆADCADC^ là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
5 tháng 10 2021
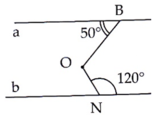
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
21 tháng 10 2021
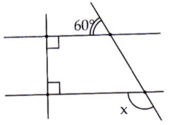
Ta có: \(\widehat{BAD}+\widehat{ABC}=110^o+70^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒a//b
a//b, b⊥d⇒a⊥d
21 tháng 10 2021
Ta có \(\widehat{BAD}\) + \(\widehat{ABC}\) = 180° => a // b
Mà \(\widehat{BCD}\) = 90°=>d ⊥ b. Do đó d ⊥ a
19 tháng 9 2018
Hình nào?
không có hình thì làm làm sao được?
Bạn vẽ hình đi :)
PT
1
6 tháng 9 2015
+) Góc xOy = 60o => góc xOy' = 120o (do kề bù với góc xOy)
=> góc x'Oy = 120o ( do đối đỉnh)
+) Oz là tia p/g của góc xOy' => góc xOz = zOy' = xOy'/2 = 60o
=> có góc x'Oz = 120o (Vì kề bù với góc zOx)
và góc yOz = 120o ( Vì yOz = yOx + xOz )
Vậy có 4 góc có số đo là 120o
a // b
=> ADC và BCD là 2 góc trong cùng phía bù nhau
=> ADC + BCD = 180o
Thay số: ADC + 120o = 180o
=> ADC = 60o