Công thức nghiệm tổng quát của phương trình 0x + 4y = −16
A. x ∈ ℝ y = − 4
B. x ∈ ℝ y = 4
C. y ∈ ℝ x = − 4
D. y ∈ ℝ x = 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 12 2019
Đáp án B
Đặt t = 2 − x + 2 + x ⇔ t 2 = 4 + 2 4 − x 2 ⇔ 4 − x 2 = t 2 − 4 2 và x ∈ − 2 ; 2 ⇒ t ∈ 2 ; 2 2
Khi đó, phương trình đã cho trở thành: t − t 2 − 4 2 = m ⇔ 2 m = − t 2 + 2 t + 4 = f t .
Xét hàm số f t = − t 2 + 3 t + 4 trên đoạn 2 ; 2 2 ⇒ min 2 ; 2 2 f t = − 4 + 4 2 ; m a x 2 ; 2 2 f t = 4
Do đó, để phương trình f t = 2 m có nghiệm ⇔ − 2 + 2 2 ≤ m ≤ 2 ⇒ a = − 2 + 2 2 b = 2
Vậy T = a + 2 2 + b − 2 + 2 2 + 2 2 + 2 = 6
CM
9 tháng 8 2017
Đáp án A
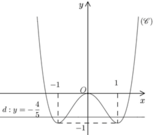
(1) là phương trình hoành độ giao điểm của (C) và đường thẳng ( d ) : y = - 4 5
Suy ra: Số nghiệm của phương trình (1) là số giao điểm của đồ thị (C) và đường thẳng (d)
CM
6 tháng 9 2019
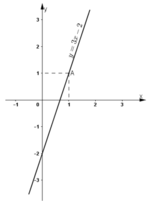
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
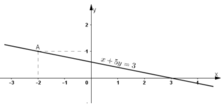
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
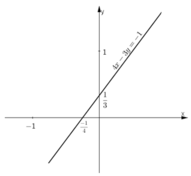
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 
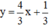
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
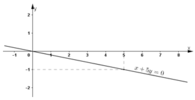
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔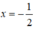 
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
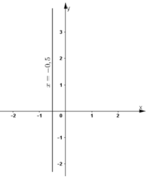
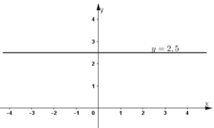
f) 0x + 2y = 5
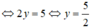
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
CM
13 tháng 7 2018
Đáp án D
Hàm số f(x) có dạng f ( x ) = ( x + 2 ) ( x - 1 ) 2 Giao với trục Oy tại (0, 2) .
=> 2<m<4.
Chọn phương án D.
9 tháng 1
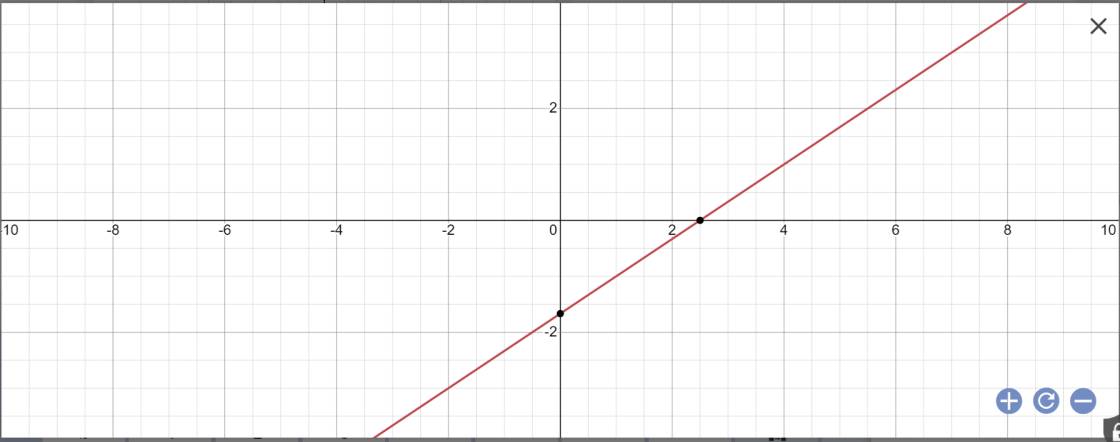
a: 2x-3y=5
=>3y=2x-5
=>\(y=\dfrac{2}{3}x-\dfrac{5}{3}\)
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x-\dfrac{5}{3}\end{matrix}\right.\)
Biểu diễn tập nghiệm:
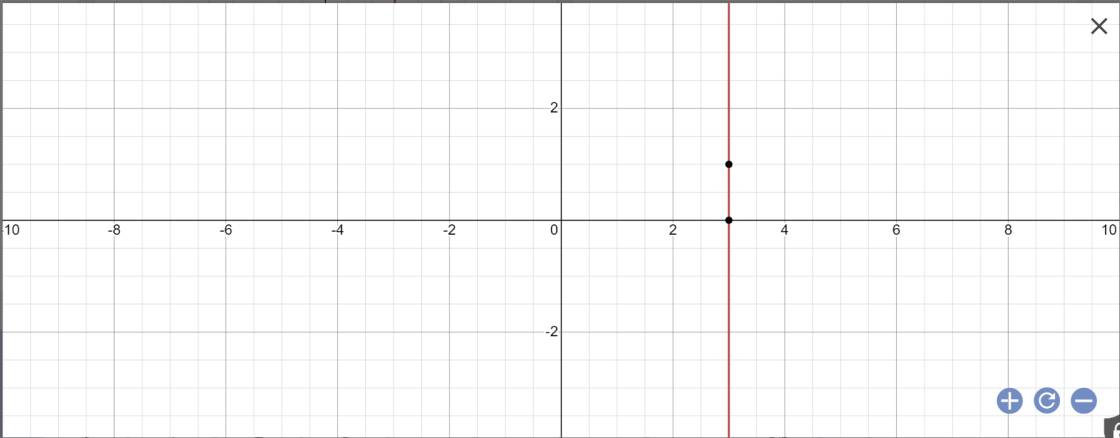
b: 4x+0y=12
=>4x=12
=>x=3
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x=3\\y\in R\end{matrix}\right.\)
Biểu diễn tập nghiệm:
c: 0x-3y=6
=>-3y=6
=>y=-2
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=-2\end{matrix}\right.\)
Biểu diễn tập nghiệm:
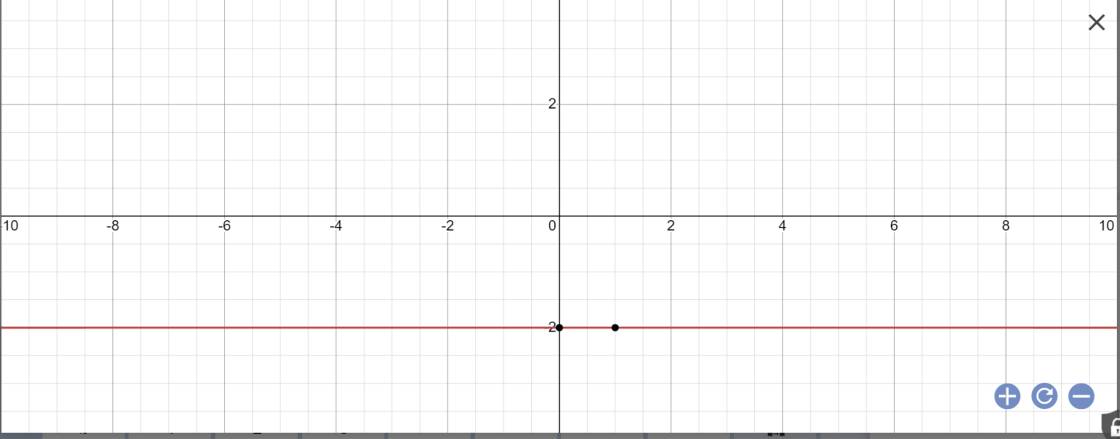
Ta có 0x + 4y = −16 ⇔ y = −4
Nghiệm tổng quát của phương trình x ∈ ℝ y = − 4
Đáp án: A