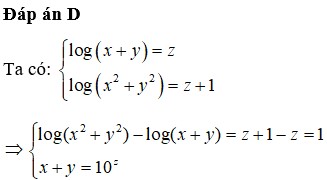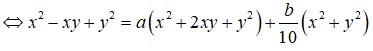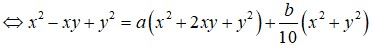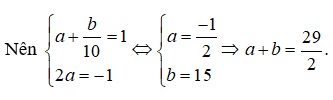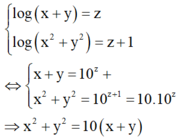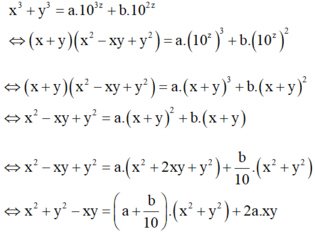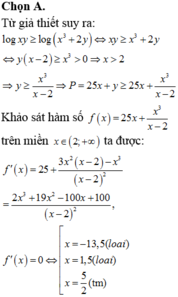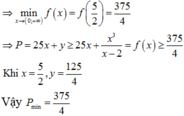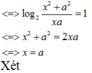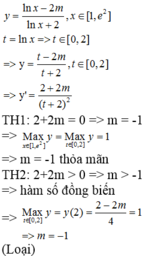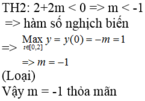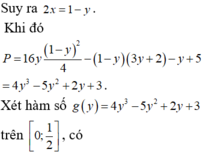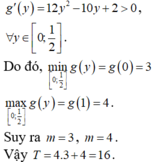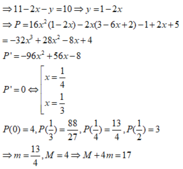Cho x, y là các số thực thỏa mãn log 2 y 2 1 + x = 3 y - 1 + x - y 2 + x . Giá trị nhỏ nhất của biểu thức P = x - y bằng
A. - 3 4
B. - 5 4
C. -2
D. -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 5 2017
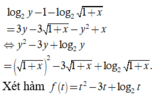
và đi đến kết quả
y
=
1
+
x
Đúng(0)
Những câu hỏi liên quan
PT
1
CM
9 tháng 11 2018
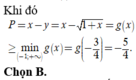
Đáp án A
Sử dụng BĐT buhinhacopski ta có
x − 2 + y + 3 2 ≤ 1 + 1 x − 2 + y + 3 = 2 x + y + 2 .
Tức là ta có x + y + 1 2 ≤ 4 2 x + y + 2 . Đặt t = x + y . Chú ý rằng t ≥ − 1 .
Ta có
t + 1 2 ≤ 8 t + 8 ⇔ t 2 − 6 t − 7 ≤ 0 ⇔ − 1 ≤ t ≤ 7.
Vậy max t = 7 xảy ra khi x − 2 = y + 3 x + y = 7 ⇔ x = 6 y = 1 .
VV
1
15 tháng 4 2020
Từ giả thiết \(x^2+y^2=1\Rightarrow y^2\le1\Rightarrow-1\le y\le1\Rightarrow y^3\le y^2\)
\(P=2x+y^3\le2x+y^2=2x+1-x^2=2-\left(x-1\right)^2\le2\)
Dấu "=" khi \(\hept{\begin{cases}x-1=0\\x^2+y^2=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=0\end{cases}}}\)