Ai chỉ mik vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 has changed
2 are driving
3 were made
4 went - saw
5 finish
6 have been
7 weren't
8 will write
9 doing
10 to work
11 will clean
12 tastes - are
13 has become
14 went
15 is learning
16 won't be
17 is cut
18 eats
19 stewing
20 to drink
21 is organised
22 built
23 were made
14 was set
25 haven't done
26 is speaking
27 are spoken

a) \(\left(2x+1\right)^2-4\left(x+2\right)^2=9\\ \Rightarrow\left(2x+1\right)^2-\left[2\left(x+2\right)\right]^2=9\\ \Rightarrow\left(2x+1-2x-4\right)\left(2x+1+2x+4\right)=9\\ \Rightarrow-3\left(4x+5\right)=9\\ \Rightarrow-12x-15=9\\ \Rightarrow x=-2\)
b) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\\ \Rightarrow x^2+6x+9-\left(x^2+4x-32\right)=1\\ \Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\\ \Rightarrow x=-20\)
\(a,\Rightarrow4x^2+4x+1-4x^2-16x-16=9\\ \Rightarrow-12x=24\Rightarrow x=-2\\ b,\Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\Rightarrow x=-20\\ c,\Rightarrow3x^2+12x+12+4x^2-4x+1-7x^2+63=36\\ \Rightarrow8x=-40\Rightarrow x=-5\\ d,\Rightarrow x^3-27+4x-x^3=1\\ \Rightarrow4x=28\Rightarrow x=7\\ e,\Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6=-19\\ \Rightarrow12x=-15\Rightarrow x=-\dfrac{5}{4}\)

Bài 3:
a: \(M=x^2-4x+5\)
\(=x^2-4x+4+1\)
\(=\left(x-2\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi x=2
b: \(N=y^2-y-3\)
\(=y^2-2\cdot y\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{13}{4}\)
\(=\left(y-\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\forall y\)
Dấu '=' xảy ra khi \(y=\dfrac{1}{2}\)

a: \(x^2-9y^2=\left(x-3y\right)\left(x+3y\right)\)
c: \(\left(x+5\right)^2-16=\left(x+1\right)\left(x+9\right)\)
e: \(\left(2x+3\right)^2-\left(x-7\right)^2\)
\(=\left(2x+3+x-7\right)\left(2x+3-x+7\right)\)
\(=\left(3x-4\right)\left(x+10\right)\)


Đừng đăng câu hỏi lung tung k liên quan đến toán và tiếng việt
Chúc bn hc tốt
Tk nha

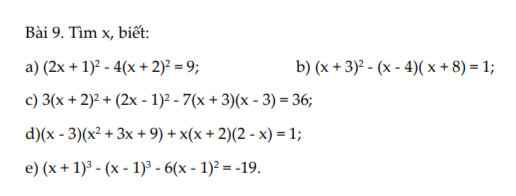
\(K=\sqrt{4x^2-4x+1} +\sqrt{4x^2-12x+9}+2\)
\(\)\(K=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}+2\)
\(K=\left|2x-1\right|+\left|2x-3\right|+2\)
\(K=\left|2x-1\right|+\left|-2x+3\right|+2\ge\left|2x-1-2x+3\right|+2\)
\(\Rightarrow K\ge\left|2\right|+2\ge4\)
\(\Rightarrow MinK=4\) \(dấu"="\) \(xảy\) \(ra\Leftrightarrow\left(2x-1\right)\left(-2x+3\right)\ge0\Leftrightarrow\dfrac{1}{2}\le x\le\dfrac{3}{2}\)