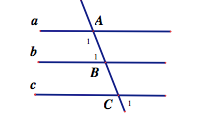
Cho hình 1.biết A1+B1=180 độ và B1=C1.Chứng minh a//b//c a b c A B C 1 1 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 1 2023
a: m vuông góc c
n vuông góc c
=>m//n
b: góc A1=180-75=105 độ
góc A2=180-105=75 độ
NL
1
26 tháng 8 2019
a A 3 2 4 1 c b B 3 2 4 1
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)
24 tháng 8 2023
a: góc A1=góc A2
mà góc A1+góc A2=180 độ(kề bù)
nên góc A1=góc A2=180/2=90 độ
=>a vuông góc c
mà b vuông góc c
nên a//b
b: góc C1=1/3*góc C2
mà góc C1+góc C2=180 độ
nên góc C1=180/4=45 độ
góc C2=180-45=135 độ
a//b
=>góc C1=góc CDB(hai góc so le trong)
=>góc CDB=45 độ
a A 1 1 B C 1 c 2
Vì \(\hept{\begin{cases}\widehat{A_1}+\widehat{B_1}=180^o\\\widehat{A_1}\text{ và }\widehat{B_1}\text{ là 2 góc trong cùng phía }\end{cases}}\Rightarrow a//b\left(1\right)\)
Vì \(\hept{\begin{cases}\widehat{B_1}=\widehat{B_2}\left(\text{ 2 góc đối đỉnh }\right)\\\widehat{C_1}=\widehat{B_1}\left(\text{bài cho}\right)\end{cases}}\Rightarrow\widehat{B_2}=\widehat{C_1}\text{ mà }\widehat{B_2}\text{ và }\widehat{C_1}\text{ là 2 góc đồng vị}\)
=> b // c ,à a // b ( chứng minh trên )
=> a // b // c
A1 + B1 = 180o
Mà A1 và B1 là 2 góc trong cùng phía
=> A1 và B1 là 2 góc trong cùng phía bù nhau
=> a // b
B1 = C1
Mà B1 và C1 là 2 góc so le ngoài
=> b // c
Mà a // b; b // c
=> a // c
=> a // b // c