lời giải chi tiết 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(a,=\dfrac{2y\left(3x-1\right)^2}{3x^2}\\ b,=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}\\ =\dfrac{2x\left(4x+4\right)}{x^2\left(x-1\right)}=\dfrac{8\left(x+1\right)}{x\left(x-1\right)}\\ c,=\dfrac{x^2+3x+4x+12}{x^2+2x+3x+6}\\ =\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+2\right)\left(x+3\right)}=\dfrac{x+4}{x+2}\)


1: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
2: Ta có: ΔABD=ΔEBD
nên DA=DE
hay D nằm trên đường trung trực của AE(1)
ta có: BA=BE
nên B nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
3: \(AD=\sqrt{BD^2-AB^2}=4\left(cm\right)\)
=>DE=4(cm)
4: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
AK=EC
Do đó: ΔADK=ΔEDC
Suy ra: \(\widehat{ADK}=\widehat{EDC}\)
=>\(\widehat{ADK}+\widehat{ADE}=180^0\)
hay K,D,E thẳng hàng

\(N=\dfrac{\dfrac{2.2}{3}\left(\dfrac{1}{5}-\dfrac{1}{7}-\dfrac{1}{11}\right)}{\dfrac{6.6}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}-\dfrac{1}{11}\right)}=\dfrac{4}{\dfrac{3}{\dfrac{36}{2}}}=24\)
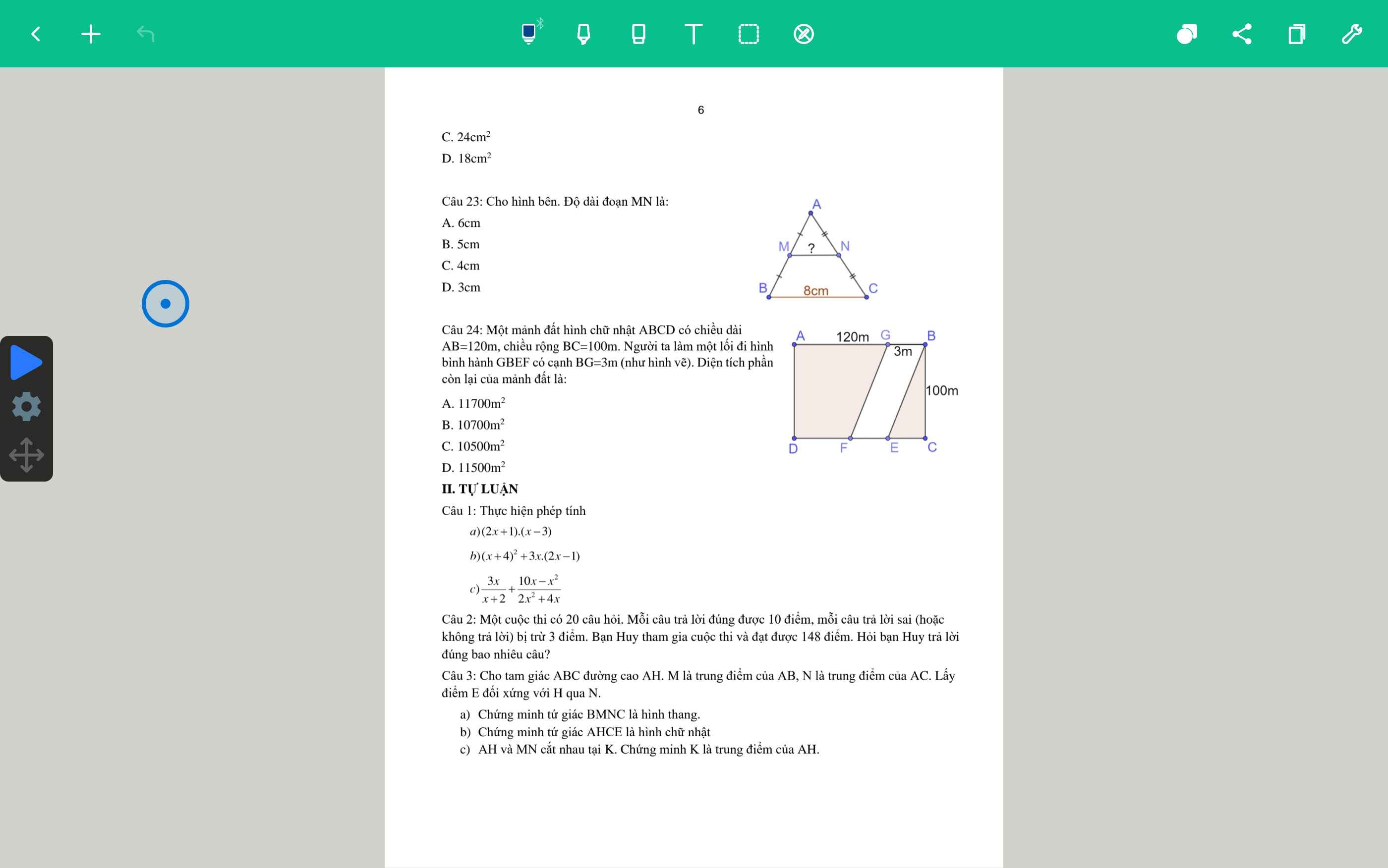
 mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn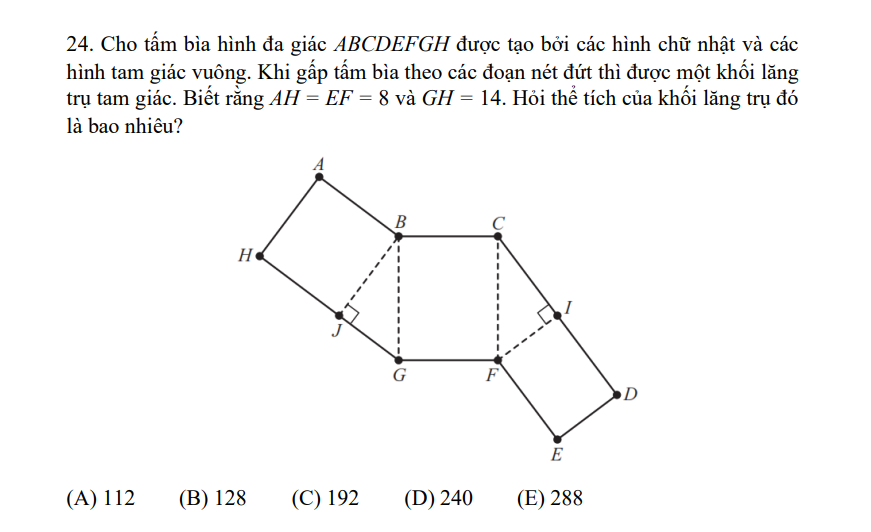


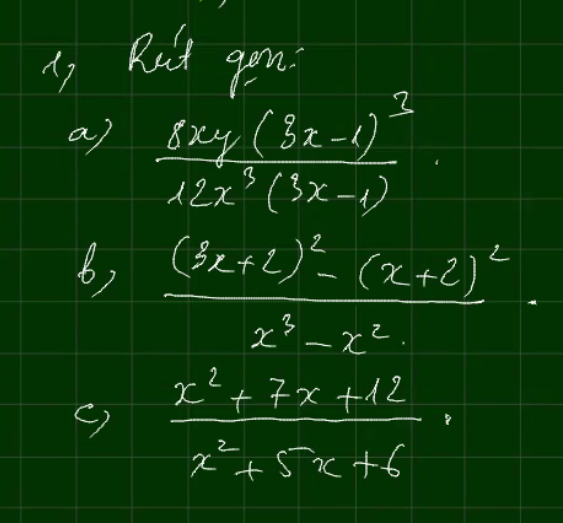

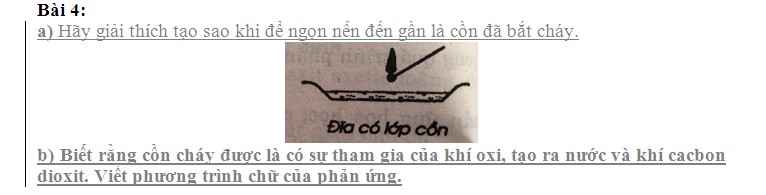
\(440+2\left(125-x\right)=546\)
\(2\left(125-x\right)=546-440\)
\(2\left(125-x\right)=106\)
\(125-x=53\)
\(x=72\)
\(846:\left[41-\left(7x-5\right)\right]=47\)
\(41-\left(7x-5\right)=846:47\)
\(41-\left(7x-5\right)=18\)
\(7x-5=23\)
\(7x=28\)
\(x=4\)