Bài 2: Cho hàm số y = 2x có đồ thị (d1); hàm số y=x-1 có đồ thị (d2) . a / Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ. b/ Xác định tọa độ giao điểm A của (d1) và (d2) bằng phép toán. c/ Viết ph / trình đường thẳng (D) song song với (d2) và điểm M(6;3) qua
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2021
b: Thay x=4 vào (d1), ta được:
\(y=\dfrac{1}{2}\cdot4=2\)
Vì (d3)//(d2) nên a=-1
Vậy: (d3): y=-x+b
Thay x=2 và y=4 vào (d3), ta được:
b-2=4
hay b=6
CM
6 tháng 6 2019
a) Tập xác định R
Bảng giá trị:
| x | 0 | -1 |
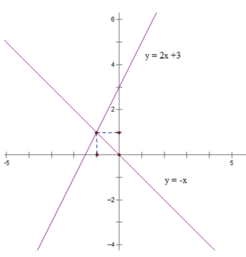
| y = 2x + 3 | 3 | 1 |
| x | 0 | -1 |
| y = - x | 0 | 1 |
20 tháng 12 2023
a: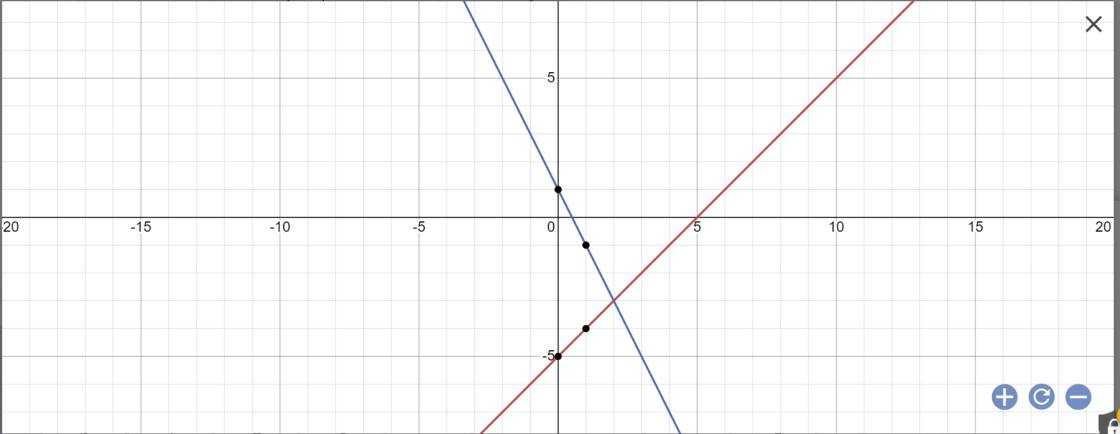 
b: Phương trình hoành độ giao điểm là:
-2x+1=x-5
=>-2x-x=-5-1
=>-3x=-6
=>x=2
Thay x=2 vào y=x-5, ta được:
\(y=2-5=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
c: (d1): y=x-5
=>x-y-5=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)
(d2): y=-2x+1
=>y+2x-1=0
=>2x+y-1=0
Khoảng cách từ O đến (d2) là:
\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)
CM
18 tháng 9 2019
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 1 |
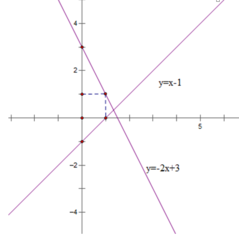
| y = -2x + 3 | 3 | 1 |
| x | 0 | 1 |
| y = x – 1 | - 1 | 0 |
CM
21 tháng 2 2017
Gọi ( x 0 , y 0 ) là tọa độ giao điểm của d 1 và d 2
Khi đó ta có:
( y 0 = 2 x 0 + 3 và y 0 = - x 0
⇒ - x 0 = 2 x 0 + 3 ⇔ 3 x 0 = -3 ⇔ x 0 = -1
⇒ y 0 = - x 0 = 1
Vậy tọa độ giao điểm của d 1 và d 2 là (- 1; 1)
3 tháng 1 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-5=\dfrac{1}{2}x\\y=2x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}x=5\\y=2x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=2\cdot\dfrac{10}{3}-5=\dfrac{20}{3}-\dfrac{15}{3}=\dfrac{5}{3}\end{matrix}\right.\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x=x-1\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Chỉ tôi câu c đc ko cậu