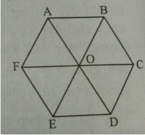
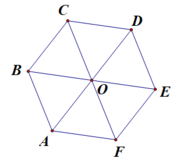
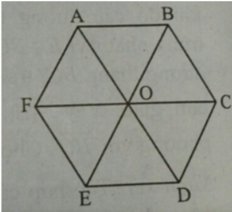
Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

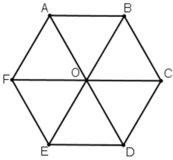
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
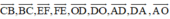
b) Các vectơ bằng vectơ AB→ là:
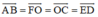

Chắc là lục giác đều?
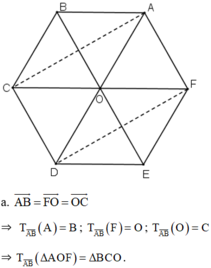
Các vecto bằng \(\overrightarrow{AB}\) là \(\overrightarrow{FO};\overrightarrow{OC};\overrightarrow{ED}\)


Do ABCDEF là lục giác đều tâm O nên AB = BC = CD= DE = EF = FA = OC.
Trên hình có tất cả 12 đoạn thẳng bằng nhau và bằng OC, tạo thành 24 vectơ có độ dài bằng OC. Trừ ra vectơ O C → còn lại 23 vectơ.
Chọn D.

Ta có: BC // AD // EF.
Do đó, các vectơ khác O A → và cùng phương với nó là:
B C → ; C B → ; O D → ; D O → ; A O → ; A D → ; D A → ; E F → ; F E →
Vậy số các vectơ khác O A → cùng phương với nó là 9 .
Chọn C.

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
Các véc tơ bằng véc tơ \(\overrightarrow{AB}\) là:
\(\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\).
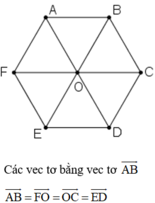
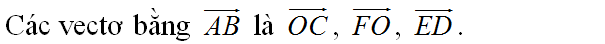
Đáp án B