Cho các điểm A, B, C, D, E, F. Khi đó E B → + D E → + A C → + B F → + C D → bằng vectơ nào trong các vectơ sau đây?
A. A E →
B. A F →
C. A D →
D. A C →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADBE có
\(\widehat{ADB}+\widehat{AEB}=90^0+90^0=180^0\)
nên ADBE là tứ giác nội tiếp
=>A,D,B,E cùng thuộc một đường tròn
b: Xét tứ giác ADCF có
\(\widehat{ADC}+\widehat{AFC}=90^0+90^0=180^0\)
nên ADCF là tứ giác nội tiếp
=>A,D,C,F cùng thuộc một đường tròn
c: Xét tứ giác BEFC có
\(\widehat{BEC}=\widehat{BFC}=90^0\)
=>BEFC là tứ giác nội tiếp
=>B,E,F,C cùng thuộc một đường tròn
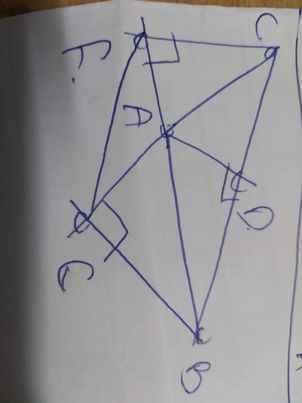

a: Ta có: ΔADB vuông tại D
=>D,A,B cùng nằm trên đường tròn đường kính AB(1)
Ta có: ΔEAB vuông tại E
=>E,A,B cùng nằm trên đường tròn đường kính AB(2)
Từ (1),(2) suy ra D,A,E,B cùng thuộc một đường tròn
b: Ta có: ΔADC vuông tại D
=>D nằm trên đường tròn đường kính AC(3)
Ta có: ΔCFA vuông tại F
=>F nằm trên đường tròn đường kính AC(4)
Từ (3) và (4) suy ra C,F,A,D cùng thuộc một đường tròn
c: Ta có:ΔCEB vuông tại E
=>E nằm trên đường tròn đường kính CB(5)
ta có: ΔCFB vuông tại F
=>F nằm trên đường tròn đường kính CB(6)
Từ (5),(6) suy ra B,C,F,E cùng thuộc một đường tròn


Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
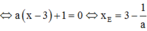
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó 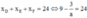
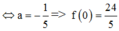

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
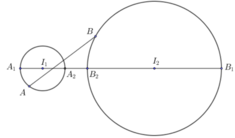
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

ĐKXĐ: \(x\ge-1\)
Đặt \(\sqrt{x+1}=y\ge0\)
\(\Rightarrow4x^2+12xy=27y^2\)
\(\Leftrightarrow\left(2x-3y\right)\left(2x+9y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3y=2x\\9y=-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\sqrt{x+1}=2x\left(x\ge0\right)\\9\sqrt{x+1}=-2x\left(x\le0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9\left(x+1\right)=4x^2\left(x\ge0\right)\\81\left(x+1\right)=4x^2\left(x\le0\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{81-9\sqrt{97}}{8}\end{matrix}\right.\)
Đáp án B