Giải bất phương trình :
x 2 - 1 x 2 - 3 - 3 x 2 + 2 x + 8 > 0
A. S = - 3 ; - 4 3 ∪ ( - 1 ; 1 )
B. S = - 3 ; - 4 3 ∪ 3 ; 2
C. ![]()
D. 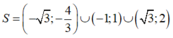
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

1a
x^2-8x<0
<=> x(x-8)<0
th1: x<0 và x-8>0
x<0 và x>8
<=> 8<x<0 ( vô lý)
th2: x>0 và x-8<0
<=> x>0 và x<8
<=> 0<x<8( tm)
vậy........
a) \(x^2-8x< 0\)
\(\Leftrightarrow x\left(x-8\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}x>0\\x-8< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x< 0\\x-8>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>0\\x< 8\end{cases}}\) hoặc \(\hept{\begin{cases}x< 0\\x>8\end{cases}}\) (loại)
\(\Leftrightarrow0< x< 8\)
b) \(x^2< 6x-5\)
\(\Leftrightarrow x^2-6x+5< 0\)
\(\Leftrightarrow x^2-x-5x+5< 0\)
\(\Leftrightarrow x\left(x-1\right)-5\left(x-1\right)< 0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-1>0\\x-5< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x-1< 0\\x-5>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1\\x< 5\end{cases}}\) hoặc \(\hept{\begin{cases}x< 1\\x>5\end{cases}}\) (loại)
\(\Leftrightarrow1< x< 5\)
c) \(\frac{x-3}{x-2}< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-3>0\\x-2< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x-3< 0\\x-2>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>3\\x< 2\end{cases}}\) (loại) hoặc \(\hept{\begin{cases}x< 3\\x>2\end{cases}}\)
\(\Leftrightarrow2< x< 3\)
d) \(\frac{x+1}{x-3}>2\) (ĐK: \(x\ne3\) )
\(\Leftrightarrow\frac{x+1}{x-3}-2>0\)
\(\Leftrightarrow\frac{x+1-2\left(x-3\right)}{x-3}>0\)
\(\Leftrightarrow\frac{-x+7}{x-3}>0\)
\(\Leftrightarrow\hept{\begin{cases}-x+7>0\\x-3>0\end{cases}}\) hoặc \(\hept{\begin{cases}-x+7< 0\\x-3< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-x>-7\\x>3\end{cases}}\) hoặc \(\hept{\begin{cases}-x< -7\\x< 3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x< 7\\x>3\end{cases}}\) hoặc \(\hept{\begin{cases}x>7\\x< 3\end{cases}}\) (loại)
\(\Leftrightarrow3< x< 7\)

Chị ơi phần a giải 2 theo 2TH. TH1 là 3 đều lớn hơn 0 và TH2 là 2 âm 1 dương
Phần b giải 3 TH: TH1 cả 3 nhỏ hơn 0
TH2 :2 dương 1 âm
TH3 : 1 âm 2 dương

BPT <=> -3x2+15x-12>0
<=> x2-5x+4<0
<=> (x-1)(x-4)<0
<=> \(\hept{\begin{cases}x-1>0\\x-4< 0\end{cases}}\)hoặc \(\hept{\begin{cases}x-1< 0\\x-4>0\end{cases}}\)(loại)
<=> 1<x<4

a, -2x>15 x>-15/2 c, th1 x+2>0 vs x+3 <0 suy ra x>-2 vs x<-3 . th2 x+2<0,x+3>0 suy ra x<-2 ,x>-3
b, 112-x2>0
x2<112 x<11
a) \(3x-8>5x+7\)
\(\Leftrightarrow-8>5x+7-3x\)
\(\Leftrightarrow-8>2x+7\)
\(\Leftrightarrow-8-7>2x\)
\(\Leftrightarrow-15>2x\)
\(\Leftrightarrow-\frac{15}{2}>x\)
\(\Rightarrow x< -\frac{15}{2}\)
b) \(\left(11-x\right)\left(11+x\right)>0\)
\(\Leftrightarrow x=\pm11\)
\(\Rightarrow-11< x< 11\)
c) \(\left(x+2\right)\left(x+3\right)< 0\)
\(\Leftrightarrow x=-2;-3\)
\(\Rightarrow-3< x< -2\)

a) \(|2x+1|=|x-3|\)
\(\Leftrightarrow|2x+1|-|x-3|=0\)
Lập bảng xét dấu :
| x | \(\frac{-1}{2}\) | 3 | |||
| 2x+1 | - | 0 | + | \(|\) | + |
| x-3 | - | \(|\) | - | 0 | + |
Nếu \(x< \frac{-1}{2}\) thì \(|2x+1|=-2x-1\)
\(|x-3|=3-x\)
\(pt\Leftrightarrow\left(-2x-1\right)-\left(3-x\right)=0\)
\(\Leftrightarrow-2x-1-3+x=0\)
\(\Leftrightarrow-x=4\)
\(\Leftrightarrow x=-4\left(tm\right)\)
Nếu \(\frac{-1}{2}\le x\le3\) thì \(|2x+1|=2x+1\)
\(|x-3|=3-x\)
\(pt\Leftrightarrow\left(2x+1\right)-\left(3-x\right)=0\)
\(\Leftrightarrow2x+1-3+x=0\)
\(\Leftrightarrow3x-2=0\)
\(x=\frac{2}{3}\left(tm\right)\)
Nếu \(x>3\) thì \(|2x+1|=2x+1\)
\(|x-3|=x-3\)
\(pt\Leftrightarrow\left(2x+1\right)-\left(x-3\right)=0\)
\(\Leftrightarrow2x+1-x+3=0\)
\(\Leftrightarrow x=-4\) ( loại )
\(x^4+x^2+6x-8=0\)
\(\Leftrightarrow\left(x^4+2x^2+1\right)-\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)^2-\left(x-3\right)^2=0\)
Mà \(\left(x^2+1\right)^2\ge0\forall x\)
\(\left(x-3\right)^2\ge0\forall x\)
Dấu bằng xảy ra khi :
\(\hept{\begin{cases}x^2+1=0\\x-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2=-1\\x=3\end{cases}}\)
Lại có \(x^2\ge0\forall x\)
\(\Leftrightarrow x^2=-1\) ( vô lí )
Vậy phương trình có tập nghiệm \(S=\left\{3\right\}\)
Chọn D
Lập bảng xét dấu
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: