Em hãy phân biệt tia số và trục số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 6 2018
Vì \(\widehat{AOB}\)và \(\widehat{BOC}\)kề bù nên \(\widehat{AOB}\)+\(\widehat{BOC}\)=\(180^0\)\(\Rightarrow5\widehat{AOB}\)+\(\widehat{AOB}\)=\(180^0\)\(\Rightarrow6\widehat{AOB}\)=\(180^0\) \(\Rightarrow\widehat{AOB}\)\(180^0:6=30^0\)
Vì \(\widehat{AOB}\)+\(\widehat{BOC}\)=\(180^0\)\(\Rightarrow30^0+\widehat{BOC}=180^0\)\(\Rightarrow\widehat{BOC}\)\(=180^0-30^0=150^0\)
b,Vì OD là phân giác của \(\widehat{BOC}\)\(\Rightarrow\)OD nằm giữa và \(\widehat{COD}=\widehat{DOB}=\frac{\widehat{BOC}}{2}=\frac{150^0}{2}=75^0\)
Vì \(\widehat{DOB}=75^0>30^0=\widehat{AOB}\)
Trên cùng nửa mặt phẳng bờ OA có \(\widehat{AOB}< \widehat{DOB}\Rightarrow OB\)nằm giữa \(OA\)và \(OD\)
\(\Rightarrow\widehat{DOB}+\widehat{AOB}=\widehat{AOD}\)
\(\Rightarrow75^0+30^0=\widehat{AOD}\)
\(\Rightarrow\widehat{AOD}=100^0\)
Phần c tự làm nhé
Học tok
VH
0
CM
30 tháng 12 2017
Đáp án B
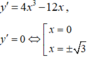
C m cắt trục hoành tại bốn điểm phân biệt khi
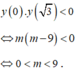
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là hoành độ giao điểm của C m với trục hoành ( x 1 < x 2 < 0 < x 3 < x 4 ).
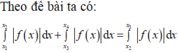
Do f(x) là hàm số chẵn và có hệ số a>0 nên
14 tháng 9 2016
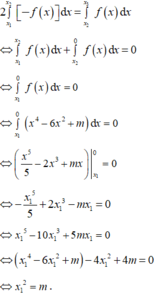
Câu 1: Sự khác nhau giữa siêu văn bản và trang web là:
- Siêu văn bản: Không gắn địa chỉ truy cập trên Internet.
- Trang web: Có gắn địa chỉ truy cập trên Internet.
Câu 2: www là địa chỉ dùng để truy cập các trang wb và khai thác tài nguyên trên Internet.
14 tháng 9 2016
oOo_tẤt cẢ đà Là QuÁ KhỨ_ oOo bạn cho mình hỏi 1 chút : Hãy nêu 1 số website mà em biết là nêu địa chỉ của website đó à bạn ?
CM
28 tháng 3 2018
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
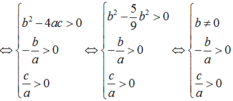
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
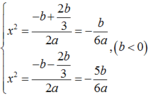
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
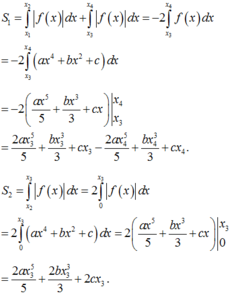
Suy ra
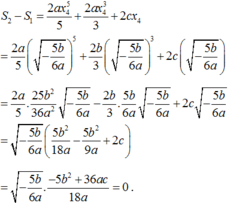
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
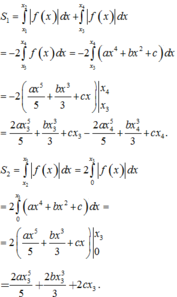
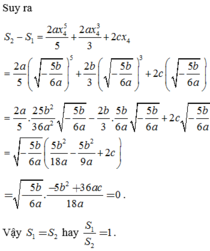
Tia số là dòng kẻ được phân ra để dễ học
Trong toán học, trục số là hình ảnh của một đường thẳng được sử dụng như là sự trừu tượng hóa cho các số thực, ký hiệu \mathbb. Mỗi điểm của trục số được giả định là tương ứng với một số thực và mỗi số thực tương ứng với một điểm trên trục số.
Trong toán học, trục số là hình ảnh của một đường thẳng được sử dụng như là sự trừu tượng hóa cho các số thực, ký hiệu {\displaystyle \mathbb {R} }. Mỗi điểm của trục số được giả định là tương ứng với một số thực và mỗi số thực tương ứng với một điểm trên trục số.[1]
Các số nguyên thường được hiển thị dưới dạng những điểm được đánh dấu đặc biệt nằm ngang trên trục số. Mặc dù hình ảnh này chỉ hiển thị các số nguyên từ -9 đến 9, trục số bao gồm tất cả số thực, tiếp tục vĩnh viễn theo cả hai hướng, và cũng có các số không được đánh dấu giữa các số nguyên. Nó thường được sử dụng như một trợ giúp trong việc giảng dạy phép cộng và phép trừ đơn giản, nhất là khi có liên quan đến các số âm.