Thể tích của khối lập phương ABCD.A'B'C'D' có đường chéo AC'= 6 bằng
A. 3 3
B. 2 3
C. 2
D. 2 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
6 tháng 4 2018
Đúng(0)
Những câu hỏi liên quan
CM
15 tháng 6 2019
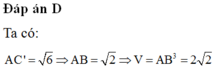
Chọn B.
Hình nón A.A'BCD' với đáy là hình chữ nhật A'BCD' có diện tích S = A'B.BC = a 2 √2 và chiều cao h = (a 2 )/2 nên có thể tích V = a 3 /3
CM
4 tháng 4 2017
Đáp án A
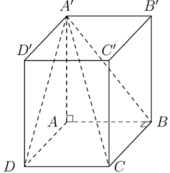
Ta có: hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3
Suy ra cạnh của hình lập phương bằng a.
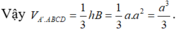Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2021
\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)
