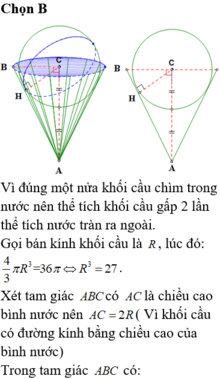
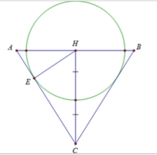
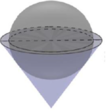
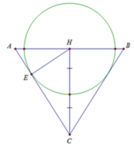
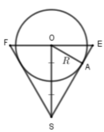
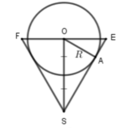
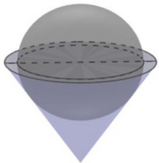
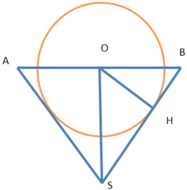
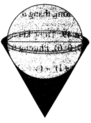
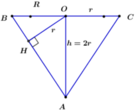
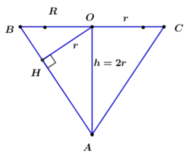
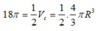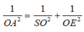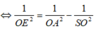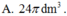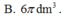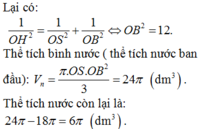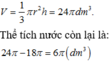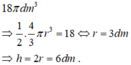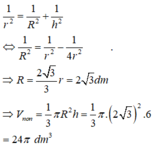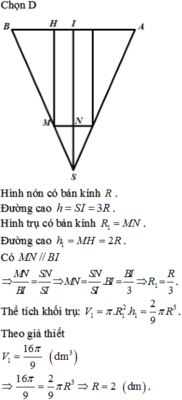Một bình đựng nước dạng hình nón (không có đáy) đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là 18 πdm 3 .Biết khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu chìm trong nước. Tính thể tích nước còn lại trong bình.
![]()
![]()
![]()
![]()