Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
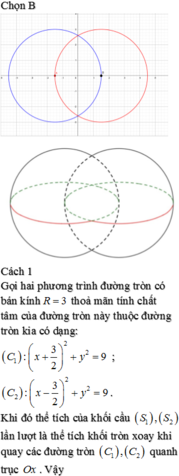
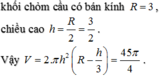
Chọn đáp án D
Giả sử mặt cầu (S) có tâm I m ; 0 ; 0 và bán kính là R (do I ∈ O x ).
Ta có
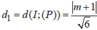
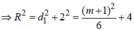
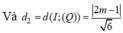
Từ đó suy ra
Để có đúng một mặt cầu (S) thỏa mãn yêu cầu khi và chỉ khi phương trình (*) có đúng một nghiệm m, tức là
Đáp án A.
Giả sử mặt cầu (S) có tâm I a ; 0 ; 0 ∈ O x , bán kính R > 0 . Khi đó phương trình mặt cầu (S) là x − a 2 + y 2 + z 2 = R 2 .
Gọi H,K lần lượt là hình chiếu của I trên (P) và (Q) , khi đó:
I H = d I ; P = a + 1 6 và I K = d I ; Q = 2 a − 1 6
Do I H 2 + 4 = R 2 và I K 2 + r 2 = R 2 nên a + 1 2 6 + 4 = R 2 2 a − 1 2 6 + r 2 = R 2
⇒ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a + 1 2 + 24 = 2 a − 1 2 + 6 r 2
⇔ a 2 − 2 a + 2 r 2 − 8 = 0 *
Để có duy nhất một mặt cầu (S) thì phương trình (*) phải có một nghiệm
⇔ Δ ' = 1 − 2 r 2 − 8 = 0 ⇔ r 2 = 9 2 . Do r > 0 nên r = 3 2 .
\(S=4\pi R^2=36\pi\Rightarrow R=3\) \(\Rightarrow OA=3\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH=2\sqrt{2}\)
Pitago tam giác vuông OAH:
\(AH=\sqrt{OA^2-OH^2}=1\)
\(\Rightarrow AB=2AH=2\)
Chọn D
Gọi I (m; 0; 0) là tâm mặt cầu có bán kính R, d1, d2 là các khoảng cách từ I đến (P) và (Q).
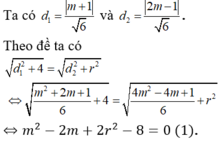
Yêu cầu bài toán tương đương phương trình (1) có đúng một nghiệm m
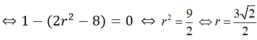
Đáp án D.
Gọi I a ; 0 ; 0 là tâm của mặt cầu (S) có bán kính R.
Khoảng cách từ tâm I đến hai mặt phẳng (P) và (Q) lần lượt là d 1 = a + 1 6 , d 2 = 2 a + 1 6
Theo giả thiết, ta có:
R 2 = d 1 2 + 2 2 = d 2 2 + r 2 ⇔ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a 2 + 2 a + 25 = 4 a 2 − 4 a + 1 + 6 r 2 ⇔ 3 a 2 − 6 a + 6 r 2 − 24 = 0 *
Yêu cầu bài toán (*) có nghiệm duy nhất
⇔ Δ ' = − 3 2 − 3 6 r 2 − 24 = 0 ⇔ r = 3 2 2 .
