Cho tam giác ABC vuông tại A. Từ A kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Khi đó ta có:
A. Tam giác BCD là tam giác nhọn
B. Tam giác BCD là tam giác vuông tại B
C. Tam giác BCD là tam giác vuông tại D
D. Tam giác BCD là tam giác vuông tại C

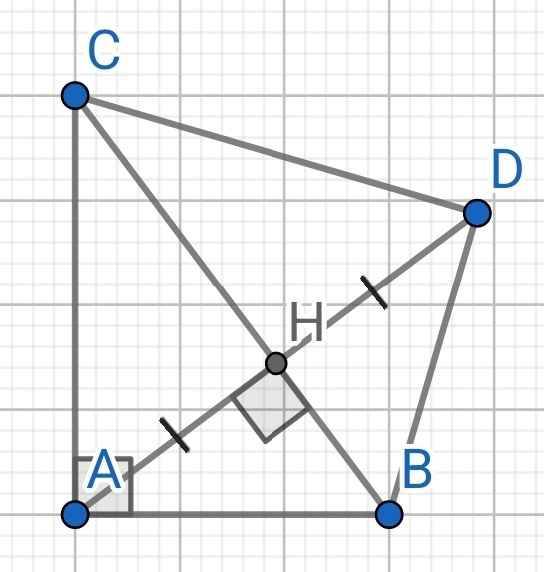
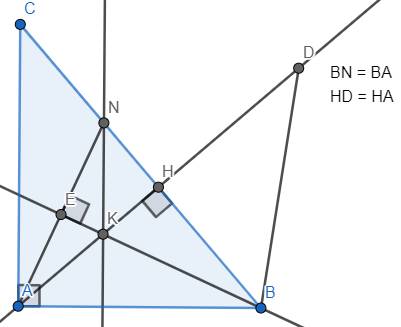
Ta có D thuộc tia đối của tia HA nên H nằm giữa hai điểm A và D
Mà HA = HD nên H là trung điểm của AD
Mặt khác B C ⊥ A D tại H (do A H ⊥ B C )
Do đó BC là đường trung trực của đoạn thẳng AD
Suy ra B A = B D C A = C D (tính chất điểm nằm trên đường trung trực của đoạn thẳng)
Xét tam giác ABC và tam giác DBC có:
BA = BD; CA = CD (cmt)
BC cạnh chung
Do đó: Δ A B C = Δ D B C (c – c – c)
Suy ra B D C ^ = B A C ^ = 90 ° (hai góc tương ứng)
Vậy tam giác BDC vuông tại D.
Chọn đáp án C