Cung AB của đường tròn (O; R) có số đo là 60 0 . Khi đó diện tích hình quạt AOB là:
A. π R 2 2
B. π R 2 6
C. π R 2 4
D. π R 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì TO là đường kính \(\Rightarrow\angle TMO=90\) mà \(M\in\left(O\right)\Rightarrow TM\) là tiếp tuyến của (O)
b) Xét \(\Delta TMC\) và \(\Delta TDM:\) Ta có: \(\left\{{}\begin{matrix}\angle MTDchung\\\angle TMC=\angle TDM\end{matrix}\right.\)
\(\Rightarrow\Delta TMD\sim\Delta TCM\left(g-g\right)\Rightarrow\dfrac{TC}{TM}=\dfrac{TM}{TD}\Rightarrow TC.TD=TM^2\)
c) Vì đường tròn đường kính TO có tâm I và đường tròn (O) cắt nhau tại M và N \(\Rightarrow\) IO là trung trực của MN \(\Rightarrow MN\bot TO\)
mà \(\Delta TMO\) vuông tại M \(\Rightarrow TM^2=TE.TO\) (hệ thức lượng)
mà \(TC.TD=TM^2\Rightarrow TC.TD=TE.TO\Rightarrow\dfrac{TC}{TE}=\dfrac{TO}{TD}\)
Xét \(\Delta TEC\) và \(\Delta TDO:\) Ta có: \(\left\{{}\begin{matrix}\angle OTDchung\\\dfrac{TC}{TE}=\dfrac{TO}{TD}\end{matrix}\right.\)
\(\Rightarrow\Delta TEC\sim\Delta TDO\left(c-g-c\right)\Rightarrow\angle TEC=\angle TDO\Rightarrow ODCE\) nội tiếp

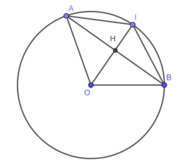
Vì I là điểm chính giữa của cung AB nên IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,I thẳng hàng

Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng
Đáp án là B