Với a là số thực dương tùy ý, l o g ( 100 a 3 ) bằng
A. 6loga
B. 3+3loga
C. 1 2 + 1 3 log a
D. 2 + 3loga
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)

Đáp án C
Vì OA, OB, OC đôi một vuông góc với nhau 1 d 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Với d là khoảng cách từ O -> (ABC) suy ra 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta có x 2 a + y 2 b + z 2 c ≥ x + y + z 2 a + b + c
Vậy d m a x = 1 3

\(\sum\dfrac{a}{\sqrt{ab+b^2}}=\sum\dfrac{a\sqrt{2}}{\sqrt{2b\left(a+b\right)}}\ge\sum\dfrac{2\sqrt{2}a}{2b+a+b}=2\sqrt{2}\sum\dfrac{a}{a+3b}\)
\(=2\sqrt{2}\sum\dfrac{a^2}{a^2+3ab}\ge\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{a^2+b^2+c^2+3\left(ab+bc+ca\right)}\)
\(=\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{\left(a+b+c\right)^2+ab+bc+ca}\ge\dfrac{2\sqrt{2}\left(a+b+c\right)^2}{\left(a+b+c\right)^2+\dfrac{1}{3}\left(a+b+c\right)^2}=\dfrac{3\sqrt{2}}{2}\)

15.
ĐKXĐ: \(x^2+2x+1>0\Rightarrow x\ne-1\)
\(\Leftrightarrow log_2\left(x^2+2x+1\right)>log_22\)
\(\Leftrightarrow x^2+2x+1>2\)
\(\Leftrightarrow x^2+2x-1>0\Rightarrow\left[{}\begin{matrix}x< -1-\sqrt{2}\\x>-1+\sqrt{2}\end{matrix}\right.\)
16.
\(J=4\int\limits^2_0f\left(x\right)dx-\int\limits^2_02xdx=4.3-x^2|^2_0=8\)
17.
\(z=2+2i-6i-6i^2=8-4i\)
\(\Rightarrow\overline{z}=8+4i\)
11.
\(S=4\pi R^2\Rightarrow R=\sqrt{\frac{S}{4\pi}}=2\left(cm\right)\)
12.
\(log\left(10a^3\right)=log10+loga^3=1+3loga\)
13.
\(S=\pi R^2\Rightarrow R=\sqrt{\frac{S}{\pi}}\)
\(\Rightarrow S_{xq}=2\pi R.l=2\pi\sqrt{\frac{S}{\pi}}.l=2l.\sqrt{\pi S}\)
14.
\(\lim\limits_{x\rightarrow-1}\frac{x-2}{x+1}=-\infty\Rightarrow x=-1\) là tiệm cận đứng

Áp dụng bất đẳng thức Bunyakovsky ta được: \(\left(ab+bc+ca+1\right)\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+1\right)\ge\left(a+b+c+1\right)^2\)\(\left(ab+bc+ca+1\right)\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}+1\right)\ge\left(b+c+a+1\right)^2\)
Cộng theo vế hai bất đẳng thức này ta được \(\left(ab+bc+ca+1\right)\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\ge2\left(a+b+c+1\right)^2\)hay \(\frac{ab+bc+ca+1}{\left(a+b+c+1\right)^2}\ge\frac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Đến đây, ta quy bất đẳng thức cần chứng minh về dạng:\(\frac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}+\frac{3}{8}\sqrt[3]{\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}}\ge1\)
Áp dụng bất đẳng thức Cauchy ta được \(\frac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}+\frac{1}{8}\sqrt[3]{\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}}\)\(\ge2\sqrt{\frac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}.\frac{1}{8}\sqrt[3]{\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}}}\)\(=\sqrt{\sqrt[3]{\frac{a^2b^2c^2}{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}}}=\sqrt[3]{\frac{abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}\)(*)
Cũng theo bất đẳng thức Cauchy ta được \(\sqrt[3]{\frac{abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}}+\frac{1}{4}\sqrt[3]{\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}}\ge2\sqrt{\frac{1}{4}}=1\)(**)
Từ (*) và (**) suy ra được \(\frac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}+\frac{3}{8}\sqrt[3]{\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}}\ge1\)
Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra a = b = c = 1

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
\(\frac{a^3}{a+2b}+\frac{b^3}{b+2c}+\frac{c^3}{c+2a}\ge\frac{\left(a^2+b^2+c^2\right)^2}{\left(a+b+c\right)^2}\)
Ta lại có \(a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\)
Do đó ta được \(\frac{a^3}{a+2b}+\frac{b^3}{b+2c}+\frac{c^3}{c+2a}\ge\frac{a^2+b^2+c^2}{3}\left(đpcm\right)\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=c\)
p/s: check
Có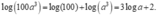
Chọn đáp án D.