Tìm tập nghiệm của bất phương trình l o g 25 x + 1 > 1 2
A. S = − 4 ; + ∞
B. S = − ∞ ; 4
C. S = − 1 ; 4
D. S = 4 ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
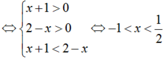

đk: \(x\ne\pm6\)
Ta có: \(\frac{x^2-3x-5}{x^2-36}\ge1\)
\(\Leftrightarrow\frac{x^2-3x-5}{x^2-36}-1\ge0\)
\(\Leftrightarrow\frac{x^2-3x-5-x^2+36}{x^2-36}\ge0\)
\(\Leftrightarrow\frac{-3x+31}{x^2-36}\ge0\)
Xét 2 TH sau:
TH1: \(\hept{\begin{cases}-3x+31\ge0\\x^2-36>0\end{cases}}\) \(\Rightarrow x\le\frac{31}{3}\) và \(\orbr{\begin{cases}x>6\\x< -6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\frac{31}{3}\ge x>6\\x< -6\end{cases}}\)
TH2: \(\hept{\begin{cases}-3x+31\le0\\x^2-36< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge\frac{31}{3}\\-6< x< 6\end{cases}}\) => Vô lý
Vậy tập nghiệm phương trình \(\orbr{\begin{cases}\frac{31}{3}\ge x>6\\x< -6\end{cases}}\)

Cái này nãy tui mới làm ở bên h_ọ_c_24 ý.
\(x\left(x-1\right)^2\ge4-x\)
\(\Leftrightarrow x\left(x^2-2x+1\right)\ge4-x\)
\(\Leftrightarrow x^3-2x^2+x\ge4-x\)
\(\Leftrightarrow x^3-2x^2+2x-4\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2\right)\ge0\)
\(\Leftrightarrow x-2\ge0\left(Vì:x^2+2>0\forall x\right)\)
\(\Leftrightarrow x\ge2\)
Vậy \(S=\left\{2;+\infty\right\}\)
@ Băng Băng @ Mình không kí hiệu tập nghiệm như vậy nhé em:
S = [ 2; \(+\infty\))

Đáp án C
B P T ⇔ x + 1 > 0 3 x − 1 > 0 x + 1 > 3 x − 1 ⇔ x > 1 3 x < 1 ⇒ S = 1 3 ; 1
Đáp án D
Bất phương trình ⇔ x + 1 > 25 1 2 = 5 ⇔ x > 4