Trong không gian Oxyz, cho đường thẳng ∆ vuông góc với mặt phẳng α : x + 2 z + 3 = 0 . Một véctơ chỉ phương của ∆ là
A. b → = 2 ; - 1 ; 0
B. v → 1 ; 2 ; 3
C. a → 1 ; 0 ; 2
D. u → 2 ; 0 ; - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng ( α ) có một véctơ pháp tuyến là n ⇀ ( 1 ; 0 ; 2 )
∆ vuông góc với ( α ) nên có véctơ chỉ phương là a ⇀ = n ⇀ = ( 1 ; 0 ; 2 )
Chọn đáp án C.

Đáp án C
Vì d ⊥ ( P ) suy ra u d → = n ( P ) → = ( 4 ; 0 ; - 1 )

Chọn C
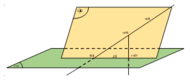
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.

Véctơ chỉ phương của d có giá song song với véctơ pháp tuyến của
( P ) , n P ⇀ = 1 ; - 1 ; 2
Đối chiếu các đáp án chọn A.
Đáp án C