Cho: 4 × a – a = 2 x 9. Giá trị của a là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 2 2019
a) \(A=\left(\frac{2+x}{2-x}-\frac{2-x}{2+x}-\frac{4x^2}{x^2-4}\right):\frac{x^2-6x+9}{\left(2-x\right)\left(x-3\right)}\)(ĐKXĐ: \(\hept{\begin{cases}x\ne\pm2\\x\ne3\end{cases}}\))\(=\left[\frac{\left(2+x\right)^2-\left(2-x\right)^2+4x^2}{4-x^2}\right]:\frac{\left(x-3\right)^2}{\left(2-x\right)\left(x-3\right)}\)\(=\frac{4x\left(x+2\right)}{\left(2-x\right)\left(x+2\right)}.\frac{2-x}{x-3}=\frac{4x}{x-3}\)
b) l\(x-5\)l\(=2\Leftrightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\left(n\right)\\x=3\left(l\right)\end{cases}\Rightarrow A=\frac{4.7}{7-3}=\frac{28}{4}=7}\)
c)
* Để A có giá trị là một số nguyên thì \(A=\frac{4x}{x-3}=\frac{4x-12+12}{x-3}=4+\frac{12}{x-3}\)là một số nguyên hay \(\frac{12}{x-3}\)là một số nguyên \(\Rightarrow x-3\inƯ\left(12\right)\Rightarrow S=\left(-9;-3;-1;0;1;4;5;6;7;9;15\right)\)(1)
* Để \(A=4+\frac{12}{x-3}< 4\Leftrightarrow\frac{12}{x-3}< 0\) thì \(x-3< 0\Leftrightarrow x< 3\)(2)
(1)(2) \(\Rightarrow S=\left(-9;-3;-1;0;1\right)\)
22 tháng 10 2023
giải phương trình
a)\(\sqrt{x^8}=256\) b)\(\sqrt{x^2-2x+1}=x-1\)
14 tháng 9 2021
ta thấy rằng 5 phải chia hết cho a tức là
a(U)5=1,-1;5,-5
vậy a 1,-1,5,-5 thì x có giá trị nguyên
29 tháng 8 2023
a: Khi x=9 thì \(A=\dfrac{17}{3+2}=\dfrac{17}{5}\)
b: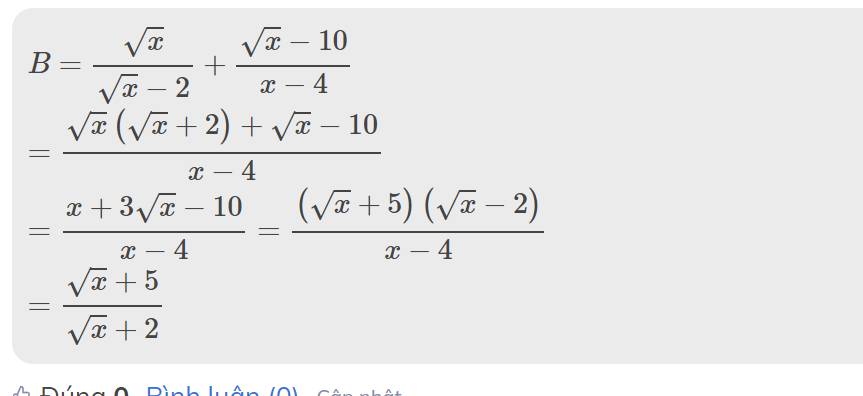 
c: P=A:B
\(=\dfrac{17}{\sqrt{x}+2}:\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{17}{\sqrt{x}+5}\)
Để P là số nguyên thì \(17⋮\sqrt{x}+5\)
mà \(\sqrt{x}+5>=5\) với mọi x thỏa mãn ĐKXĐ
nên \(\sqrt{x}+5=17\)
=>x=144
14 tháng 12 2018
a,ĐK: \(\hept{\begin{cases}x\ne0\\x\ne\pm3\end{cases}}\)
b, \(A=\left(\frac{9}{x\left(x-3\right)\left(x+3\right)}+\frac{1}{x+3}\right):\left(\frac{x-3}{x\left(x+3\right)}-\frac{x}{3\left(x+3\right)}\right)\)
\(=\frac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\frac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)
\(=\frac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}.\frac{3x\left(x+3\right)}{-x^2+3x-9}=\frac{-3}{x-3}\)
c, Với x = 4 thỏa mãn ĐKXĐ thì
\(A=\frac{-3}{4-3}=-3\)
d, \(A\in Z\Rightarrow-3⋮\left(x-3\right)\)
\(\Rightarrow x-3\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\Rightarrow x\in\left\{0;2;4;6\right\}\)
Mà \(x\ne0\Rightarrow x\in\left\{2;4;6\right\}\)
CM
24 tháng 3 2017
Ta có: |x| ≤ 4 ⇔ -4 ≤ x ≤ 4
Các số trong tập hợp A là nghiệm của bất phương trình là:
-4; -3; -2; -1; 0; 1; 2; 3; 4
7 tháng 9 2021
Bài 5:
a: Thay \(x=4+2\sqrt{3}\) vào E, ta được:
\(E=\dfrac{\sqrt{3}+1-1}{\sqrt{3}+1-3}=\dfrac{\sqrt{3}}{\sqrt{3}-2}=-3-2\sqrt{3}\)
b: Để E<1 thì E-1<0
\(\Leftrightarrow\dfrac{\sqrt{x}-1-\sqrt{x}+3}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
hay x<9
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)
c: Để E nguyên thì \(4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;5;7\right\}\)
hay \(x\in\left\{16;25;49\right\}\)
NT
7 tháng 9 2021
Câu 2:
a) Ta có \(x=4-2\sqrt{3}\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-2\right)^2}=\sqrt{3}-2\)
Thay \(x=\sqrt{3}-1\) vào \(B\), ta được
\(B=\dfrac{\sqrt{3}-1-2}{\sqrt{3}-1+1}=\dfrac{\sqrt{3}-3}{\sqrt{3}}=1-\sqrt{3}\)
b) Để \(B\) âm thì \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< 0\) mà \(\sqrt{x}+1\ge1>0\forall x\) \(\Rightarrow\sqrt{x}-2< 0\Rightarrow\sqrt{x}< 2\Rightarrow x< 4\)
c) Ta có \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=1-\dfrac{3}{\sqrt{x}+1}\)
Với mọi \(x\ge0\) thì \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Rightarrow\dfrac{3}{\sqrt{x}+1}\le3\Rightarrow B=1-\dfrac{3}{\sqrt{x}+1}\ge-2\)
Dấu "=" xảy ra khi \(\sqrt{x}+1=1\Leftrightarrow x=0\)
Vậy \(B_{min}=-2\) khi \(x=0\)
4 × a – a = 2 x 9
4 × a - 1 x a = 18
(4 - 1) x a = 18
3 x a = 18
a = 18 : 3
a = 6