Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của đoạn thẳng SA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, hãy tìm giao điểm của đường thẳng SO với mặt phẳng (MNP).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
17 tháng 12 2020
Gọi Q là trung điểm SB
Khi đó PQ||AB||MN
Mà \(P\in mp\left(MNP\right)\)
=> \(Q\in mp\left(MNP\right)\)
Khi đó tứ giác MNPQ là thiết diện cần tìm
27 tháng 8 2021
a, Mình nghĩ ý bạn là (MNP)
Trong (ABCD) gọi E = \(NP\cap BD\)
⇒ E ∈ (SBD)
Do K ∈ SD ⇒ K ∈ (SBD). M là trung điểm của SB ⇒ M ∈ (SBD)
Trong (SBD) gọi F = BK \(\cap\) ME
⇒ \(\left\{{}\begin{matrix}F\in BK\\F\in\left(MNP\right)\end{matrix}\right.\) ⇒ F = BK \(\cap\) (MNP)
b, Trong (ABCD) gọi O = AC \(\cap\) BD và H = BN \(\cap\) AC
Trong (SBD) gọi G = BK \(\cap\) SO
Trong (SAC) gọi I = SA \(\cap\) HG
(BNK) \(\cap\) (SAD) = IK
(BNK) \(\cap\) (SCD) = KN
(BNK) \(\cap\) (ABCD) = NB
(BNK) \(\cap\) (SAD) = BI
⇒ Thiết diện tạo bởi hình chóp S.ABCD và (BNK) là tứ giác IKNB
CM
15 tháng 2 2017
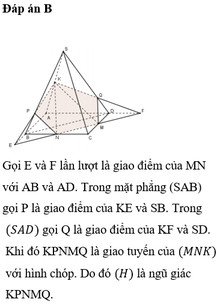
Đáp án B
Gọi P = M N ∩ A C ; I = P K ∩ S O
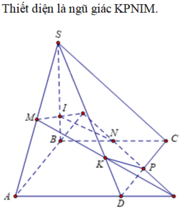
Do M N / / B D nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD, SB lần lượt tại E và F khi đó thiết diện là ngũ giác K E M N F
CM
12 tháng 4 2017
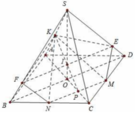
Do MN//BD nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD,SB lần lượt tại E và F khi đó thiết diện là ngũ giác KEMNF
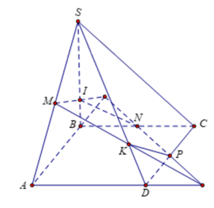
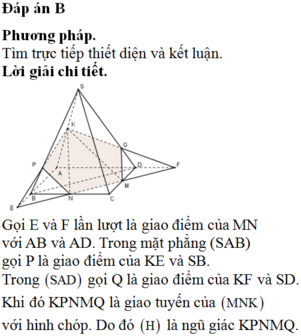
a) Tìm thiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
Vậy I = SO ∩ (MNP).