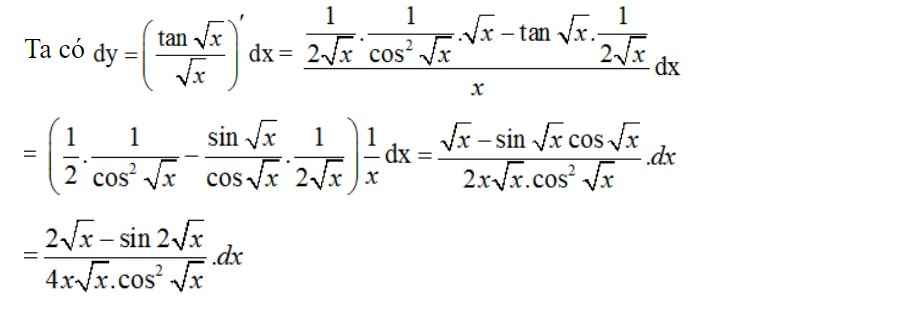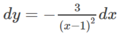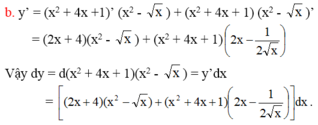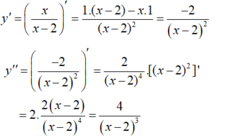Tìm vi phân của hàm số sau: y = tan x x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
22 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
SG
1
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
1.
\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)
2.
\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)
3.
\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)
CM
11 tháng 7 2018
Ta có f ' ( x ) = 2. ( x − 1 ) . ( x − 1 ) ' = 2 ( x − 1 ) nên vi phân của hàm số đã cho là:
d y = f ' x d x = 2 x − 1 d x .
Chọn đáp án A
CM
24 tháng 6 2019
Ta có:
f ' x = − 1 ( 3 x + 1 ) − 3 ( 2 − x ) ( 3 x + 1 ) 2 = − 7 3 x + 1 2
⇒ f '' x = 7. 2 3 x + 1 . 3 x + 1 ' 3 x + 1 4 = 42 3 x + 1 3
.Chọn đáp án C
CM
20 tháng 7 2019
y ' = 3 cos 2 ( 1 − x ) . [cos(1- x)] ' = 3 cos 2 ( 1 − x ) . [ − sin ( 1 − x ) ] . ( 1 − x ) ' = 3 cos 2 ( 1 − x ) . [ − sin ( 1 − x ) ] . ( − 1 ) = 3 cos 2 ( 1 − x ) . sin ( 1 − x )
Do đó, vi phân của hàm số đã cho là: d y = 3 cos 2 ( 1 − x ) . sin ( 1 − x ) d x
Chọn B