Giải các bất phương trình: 4x – 5 < 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
PT
1
9 tháng 3 2023
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
22 tháng 7 2021
1) Ta có: \(4x+8=3x-1\)
\(\Leftrightarrow4x-3x=-1-8\)
\(\Leftrightarrow x=-9\)
2) Ta có: \(10-5\left(x+3\right)>3\left(x-1\right)\)
\(\Leftrightarrow10-5x-15-3x+3>0\)
\(\Leftrightarrow-8x>2\)
hay \(x< \dfrac{-1}{4}\)
DA
2
HN
23 tháng 8 2021
Mình làm bừa thôi :>
\(\left|2x-1\right|\ge x-1\)
\(\Leftrightarrow\left|2x-1\right|-x\ge1\)
\(\Leftrightarrow\hept{\begin{cases}2x-1-x\ge-1\\-\left(2x-1\right)-x\ge-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x-1\ge0\\2x-1< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge0\\x\le\frac{2}{3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge\frac{1}{2}\\x< \frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\in\left\{\frac{1}{2};+\infty\right\}\\x\in\left\{-\infty;\frac{1}{2}\right\}\end{cases}}\)
\(\Leftrightarrow x\inℝ\)
29 tháng 8 2021
a: Ta có: \(3x+5\le4x-9\)
\(\Leftrightarrow-x\le-14\)
\(\Leftrightarrow x\ge14\)
b: Ta có: \(6-2x< 6-x\)
\(\Leftrightarrow-x< 0\)
hay x>0
c: Ta có: \(7\left(x-1\right)+5>-3x\)
\(\Leftrightarrow7x-7+5+3x>0\)
\(\Leftrightarrow10x>2\)
hay \(x>\dfrac{1}{5}\)
CM
8 tháng 9 2018
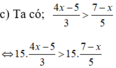
( nhân cả hai vế với 15 > 0)
⇔ 5( 4x – 5) > 3( 7- x)
⇔ 20x – 25 > 21 – 3x
⇔ 20x + 3x > 21 + 25 (chuyển vế hạng tử - 25; - 3x)
⇔ 23 x > 46
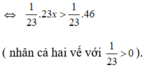
⇔ x > 2
Vậy nghiệm của bất phương trình đã cho là x > 2 .
Ta có: 4x – 5 < 7 ⇔ 4x < 7 + 5 ⇔ 4x < 12 ⇔ x < 3
Vậy tập nghiệm của bất phương trình là: {x|x < 3}