Cho hình vẽ, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:

Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD( = AB ) (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
+) Ta có AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).
Bài 2:

Ta có: DE //AB (gt) hay DE //AF
Và DF //AC (gt) hay DF //AE
Suy ra, tứ giác AEDF là hình bình hành.
Lại có, I là trung điểm của AD nên I cũng là trung điểm EF (tính chất hình bình hành)
Vậy E và F đối xứng qua tâm I.

A B C D M N I K
nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)

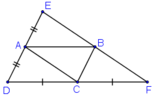
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B

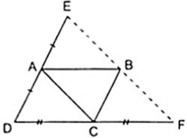
Theo giả thiết ta có:
+ A là trung điểm của DE thì AD = AE ( 1 )
+ C là trung điểm của DF thì CD = CF ( 2 )
Ta có ABCD là hình bình hành nên AD//BC
⇒ AE//BC ( 3 ) và AD = BC ( 4 )
Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )
Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
Áp dụng tính chất và định nghĩa về hình bình hành ACBE ta được 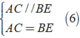
Chứng minh tương tự, tứ giác ACBF là hình bình hành
Ta được: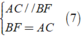
Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.

Giải :
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B

Bài giải:
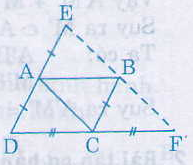
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B.


Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD( = AB ) (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
+) Ta có AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).