Vệ tinh nhân tạo của trái đất ở độ cao h = 320 km bay với vận tốc 7,9km/h. Tính tốc độ góc, chu kì, tần số của nó. Coi chuyển động là tròn đều. Bán kính Trái Đất R = 6400 km.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 1 2017
Lực hấp dẫn giữa vệ tinh và Trái Đất đóng vai trò là lực hướng tâm, ta có: Fhd = Fht
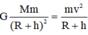
(Bán kính quỹ đạo tròn của vệ tinh từ vệ tinh đến tâm Trái Đất: R + h)
Mặt khác:
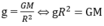
(M là khối lượng trái đất)
24 tháng 10 2021
Một vòng quay hết 90 phút=5400s \(\Rightarrow f=\dfrac{1}{5400}\)(vòng/s)
Chu kì quay: \(T=\dfrac{1}{f}=5400\left(s\right)\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{5400}=\dfrac{1}{2700}\pi\)(rad/s)
\(R=6380km=638\cdot10^5\left(m\right)\)
Tốc độ dài: \(v=\omega\cdot R=\dfrac{1}{2700}\pi\cdot638\cdot10^5\approx74234,671\)m/s
Gia tốc hướng tâm: \(a_{ht}=r\cdot\omega^2=638\cdot10^5\cdot\left(\dfrac{1}{2700}\pi\right)^2\approx86,37\)m/s2
H9
HT.Phong (9A5)
CTVHS
15 tháng 4 2023
a. Ta có: \(8km/s=8000m/s\)
Khoảng cách từ vệ tinh đến trái đất:
\(r=\left(600.10^3\right)+\left(6400.10^3\right)=7.10^6m\)
Tốc độ góc của vệ tinh bạy 1 vòng trái đất:
\(\omega=\dfrac{v}{r}=\dfrac{8000}{7.10^6}=\dfrac{1}{875}\left(rad/s\right)\)
b. Chu kì của vệ tinh bay hết một vòng trái đất:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2.3,14}{\dfrac{1}{875}}=5495s\)
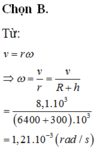
Tốc độ góc ω = v R + h = 7 , 9 6400 + 320 = 8 , 2.10 − 4 s-1.
Chu kì T = 2 π ω = 2.3 , 14 8 , 2.10 − 4 = 7658 s = 2h 7 phút 38 giây.
Tần số f = 1 T = 1 7658 = 0 , 13.10 − 3 vòng/giây.