Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau:
1 x < 1 - 1 x + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
6 tháng 9 2017
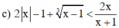
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}
MN
5 tháng 6 2020
\(\left(x+1\right)\left(x-1\right)< 0\)
\(\Leftrightarrow x^2-1< 0\)
\(\Leftrightarrow x^2< 1\)
\(\Leftrightarrow\hept{\begin{cases}x< 1\\x>-1\end{cases}}\)
Vậy giá trị thỏa mãn của x là 0
CM
5 tháng 5 2018
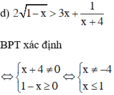
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.
CM
21 tháng 9 2018
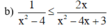
BPT xác định khi
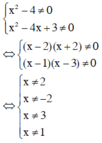
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}
HQ
17 tháng 2 2021
\(\left\{{}\begin{matrix}mx+y=3\left(1\right)\\4x+my=6\left(2\right)\end{matrix}\right.\)
TH1: m=0 có nghiệm:\(\left\{{}\begin{matrix}x=\dfrac{6}{4}\\y=3\end{matrix}\right.\) ( Thỏa mãn điều kiện đề bài ) => nhận m=0
TH2: m khác 0 \(\dfrac{m}{4}\ne\dfrac{1}{m}\Leftrightarrow m\ne\pm2\)
\(\left\{{}\begin{matrix}\left(1\right)\Rightarrow y=3-mx\\\left(2\right)\Rightarrow x=\dfrac{6-my}{4}=\dfrac{6-m\left(3-mx\right)}{4}\end{matrix}\right.\)
\(\Rightarrow\left(m^2-4\right)x=3m-6\) \(\Rightarrow x=\dfrac{3}{m+2}\) đối chiếu điều kiện: (x>1)
\(\Rightarrow\dfrac{3}{m+2}-1>0\) \(\Leftrightarrow\dfrac{1-m}{m+2}>0\)
TH1: \(\left\{{}\begin{matrix}1-m< 0\\m+2< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\) ( Loại )
TH2: \(\left\{{}\begin{matrix}1-m>0\\m+2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>-2\end{matrix}\right.\) ( Nhận ) \(\Rightarrow m\in\left(-2;1\right)\)
Đối chiếu điều kiện: y>0 \(\Leftrightarrow3-m\left(\dfrac{3}{m+2}\right)>0\)
\(\Leftrightarrow\dfrac{2}{m+2}>0\) \(\Leftrightarrow m>-2\)
Gộp cả 2 điều kiện x và y ta được m=-1 và m=0
Nãy giờ gõ nó cứ bị lỗi :D
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}