Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng: ∠A = ∠B + ∠C.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 5 2018
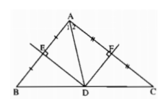
Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
DD
3 tháng 5 2019
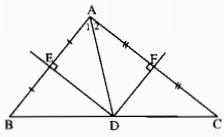
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b)
Ta có ∆DEB = ∆DEA(c.g.c) nên ˆB=ˆA1B^=A1^. Tương tự ˆC=ˆA2C^=A2^.
Suy ra ˆA=ˆA1+ˆA2=ˆB+ˆC
3 tháng 4 2018
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có: Tam giác DEA = tam giác DEA (c.g.c) nên góc B = góc A1
<=> góc C = góc A2
=> Góc A = góc A1 + góc A2 = góc B + góc C.
3 tháng 4 2017
a) Vì D là điểm chung của 2 dường trung trực
=>D là điểm chung của 3 đường trung trực (tính đồng quy trong tam giác)
=>D thuộc trung trực ứng với cạnh BC mà D thuộc BC
=> D là trung điểm của cạnh BC (đpcm)
b) Nối AD
Vì D là điểm chung của 3 trung trực (câu a) mà D thuộc BC
=> tam giác ABC vuông tại A (tam giác có tâm đường tròn ngoại tiếp thuộc 1 cạnh của tam giác ấy là tam giác vuông)
=>góc B +góc C = góc A = 90 độ (t/c tam giác vuông) (đpcm)
28 tháng 5 2020
ôi dào , bài nhu thế này ta ko bt làm , phải làm sao đây ....?
26 tháng 2 2017
Xét hai tam giác ABE và DCE có AB=DC (giả thiết), BE=CE (vì E nằm trên trung trực BC) và EA=ED (vì E nằm trên trung trực CD). Suy ra hai tam giác bằng nhau theo trường hợp c.c.c. Từ đó suy ra góc ABE= góc DCE = góc ACE. Vậy B,C nhìn AE dưới hai góc bằng nhau, do đó ABCE nội tiếp. Suy ra E nằm trên đường tròn ngoại tiếp tam giác ABC.
+) Xét tam giác ADE và BDE có:
DE chung
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
Từ (1) và (2) suy ra: