Nêu định nghĩa các hàm số lượng giác. Chỉ rõ tập xác định và tập giá trị của từng hàm số đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Ví dụ hàm số $y=\frac{-1}{2}x$
Ta có bảng sau:
Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số
Tập xác định của hàm số \(D = \left\{ { - 2; - 1; - \frac{1}{2};0;\frac{1}{2};1;2} \right\}\)
Tập giá trị của hàm số \(\left\{ {1;\frac{1}{2};\frac{1}{4};0; - \frac{1}{4}; - \frac{1}{2}; - 1} \right\}\)
CM
19 tháng 1 2017
Đáp án B
Điều kiện: x ≠ − m 2 .
y ' = m 2 − 4 2 x + m 2 ;
Hàm số đồng biến trên từng khoảng thuộc tập xác định
⇔ y ' > 0, ∀ x ≠ − m 2 ⇔ m 2 − 4 > 0, ∀ x ≠ − m 2 ⇔ m > 2.
15 tháng 8 2023
Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C
CM
4 tháng 6 2019
Đáp án C
Ta có y ' = − m 2 + 2016 m + 2017 x + m 2 , y ' = 0 đồng biến trên từng khoảng xác định nếu
y ' > 0 ∀ x ∈ D ⇔ − m 2 + 2016 m + 2017 > 0 ⇔ m ∈ − 1 ; 2017
Ta đếm số nguyên trong
− 1 ; 2017 thì có 2016 số nguyên trong đó.
24 tháng 9 2023
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
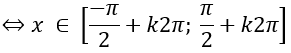
a. Định nghĩa 1 : (Hàm số sin): Quy tắc tương ứng với mỗi số thực x với số thực sinx.
sin: R -> R
x -> y = sinx.
Hàm số y = sinx có tập xác định là R, tập giá trị là đoạn [-1;1].
b.Định nghĩa 2 : (Hàm số cosin): Quy tắc tương ứng với mỗi số thực x với số thực cosx.
cos : R -> R
x -> y = cosx.
Hàm số y = cosx có tập xác định là R, tập giá trị là đoạn [-1;1]
c. Định nghĩa 3: (Hàm số tang): Hàm số tang là hàm số được xác định bởi công thức
tan : D -> R
x -> y = tanx.
Hàm số y = tanx có tập xác định: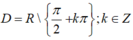
Tập giá trị của hàm số y = tanx là R.
d. Định nghĩa 4 : (Hàm số cotang): là hàm số được xác định bởi công thức
cot : D -> R
x -> y = cotx.
Hàm số y = cotx có tập xác định D = {x ∈ R \ x ≠ kπ, k ∈ Z}. Tập giá trị của hàm số y = cotx là tập R.