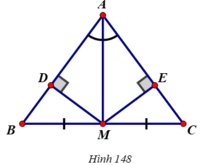
Tìm các tam giác bằng nhau trên hình 148.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
7
20 tháng 4 2017
Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn^A1 = ^A2)
∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.
MD=ME, do ∆AMD=∆AME)
∆AMB= ∆AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
LH
20 tháng 4 2017
Ta có: \(\Delta\)AMD=\(\Delta\)AME(Cạnh huyền AM chung, góc nhọn \(\widehat{A}_1=\widehat{A}_2\))
\(\Delta\)MDB=\(\Delta\)MEC(Cạnh huyền BM=CM, cạnh góc vuông )
MD=ME, do \(\Delta\)AMD=\(\Delta\)AME)
\(\Delta\)AMB= \(\Delta\)AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
CM
19 tháng 1 2019
- Xem hình 63)
Ta có:
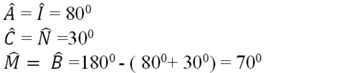
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO
- Xem hình 64)
ΔPQR có:
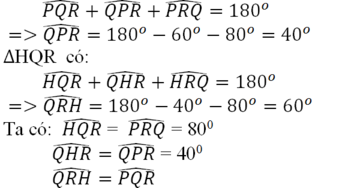
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
2 tháng 6 2017
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH
13 tháng 6 2016
A B H C 1 2
a) Tam giác ABC vuông tại A nên có +
= 900
Hay ,
phụ nhau, tam giác AHB vuông tại H nên có
+
= 900
hay ,
phụ nhau. Tam giác AHC vuông tại H nên có
+
= 900
hay ,
phụ nhau.
b) Ta có +
= 900
+
= 900
=> =
+
= 900
và +
= 900
=> =
13 tháng 6 2016
A B C H
A) các cặp góc phụ nhau : góc BAH và góc ABH ; góc HAC và góc HCA; góc ABC và góc ACB
B) các cặp góc nhọn bằng nhau : góc HCA và góc HBA ; góc HAC và góc HAB; góc ACH và góc ABH
PT
1
CM
30 tháng 4 2018
- Trong ΔDEK có:
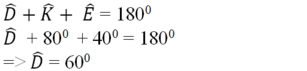
- Xét ΔABC và ΔKDE có:
AB = KD (gt)
BC = DE (gt)
Do đó ΔABC = ΔKDE
- Xét ΔMNP và ΔABC có:
MN = AB
NP = BC
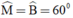nhưng góc M và góc B không xen giữa hai cạnh bằng nhau.
⇒ ΔMNP không bằng ΔABC
⇒ ΔMNP cũng không bằng ΔKDE.
+ Hai tam giác vuông AMD và AME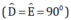
có:
AM chung
⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)
⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)
+ Hai tam giác vuông MDB và MEC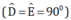
có
MB = MC (GT)
MD = ME (chứng minh trên)
⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)
⇒ BD=CE ( hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.
+ Xét ΔAMB và ΔAMC có:
MB = MC (GT)
AB = AC (chứng minh trên)
AM chung
⇒ ΔAMB = ΔAMC (c.c.c)