So sánh x và y trong mỗi trường hợp sau:
a) x − 2 3 ≤ y − 2 3 ; b) − 3 − x > − y − 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
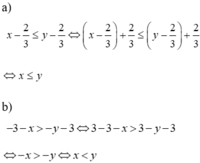
a) Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.1 + ( - 1).1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {1^2}} }} = 0 \Rightarrow {d_1} \bot {d_2}\)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc với nhau tại điểm có tọa độ \(( - 3; - 1)\)
b) Đường thẳng \({d_1}\) có phương trình tổng quát là: \({d_1}:2x - y + 1 = 0\)
Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}2x - y + 1 = 0\\x - 3y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{1}{5}\\y = \frac{3}{5}\end{array} \right.\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {2.\left( { - 1} \right) + 1.( - 3)} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {{d_1},{d_2}} \right) = 45^\circ \)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau tại điểm có tọa độ \(\left( { - \frac{1}{5};\frac{3}{5}} \right)\) và góc giữa chúng là \(45^\circ \)
c) Đường thẳng \({d_1}\) và \({d_2}\) lần lượt có phương trình tổng quát là:
\({d_1}:3x + y - 11 = 0,{d_2}:x - 3y + 8 = 0\)
Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}3x + y - 11 = 0\\x - 3y + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = \frac{7}{2}\end{array} \right.\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {3.1 + 1.( - 3)} \right|}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = 0 \Rightarrow \left( {{d_1},{d_2}} \right) = 90^\circ \)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc tại điểm có tọa độ \(\left( {\frac{5}{2};\frac{7}{2}} \right)\)
9 tháng 11 2017
Lộn, lộn,
\(3^{450}=\left(3^3\right)^{150}=27^{150}\)
Vì \(27^{150}>25^{150}\)nên \(A>B\)
9 tháng 11 2017
1) Ta có: \(3^{450}=\left(3^3\right)^{150}=9^{150}\).
\(5^{300}=\left(5^2\right)^{150}=25^{150}\)
Ví \(9^{150}< 25^{150}\)nên \(3^{450}< 5^{300}\)
\(\Rightarrow A< B\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Ta có:
\(2p = \;\frac{5}{2} \Rightarrow p = \frac{5}{4} \Rightarrow \frac{p}{2} = \frac{5}{8}\).
Tiêu điểm của parabol là: \(F\left( {\frac{5}{8};0} \right)\)
Phương trình đường chuẩn là: \(x + \frac{5}{8} = 0\)
b) Ta có:
\(2p = 2\sqrt 2 \Rightarrow p = \sqrt 2 \Rightarrow \frac{p}{2} = \frac{{\sqrt 2 }}{2}\).
Tiêu điểm của parabol là: \(F(\frac{{\sqrt 2 }}{2};0)\)
Phương trình đường chuẩn là: \(x + \frac{{\sqrt 2 }}{2} = 0\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Thay tọa độ điểm \(M\left( {1;12} \right)\) và \(N\left( { - 3;4} \right)\) ta được:
\(\begin{array}{l}\left\{ \begin{array}{l}a{.1^2} + b.1 + 4 = 12\\a.{\left( { - 3} \right)^2} + b.\left( { - 3} \right) + 4 = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a + b = 8\\9a - 3b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 6\end{array} \right.\end{array}\)
Vậy parabol là \(y = 2{x^2} + 6x + 4\)
b) Hoành độ đỉnh của parabol là \(x_I = \frac{{ - b}}{{2a}}\)
Suy ra \(x_I = \frac{{ - b}}{{2a}} = - 3 \Leftrightarrow b = 6a\) (1)
Thay tọa độ điểm I vào ta được:
\(\begin{array}{l} - 5 = a.{\left( { - 3} \right)^2} + b.\left( { - 3} \right) + 4\\ \Leftrightarrow 9a - 3b = - 9\\ \Leftrightarrow 3a - b = - 3\left( 2 \right)\end{array}\)
Từ (1) và (2) ta được hệ
\(\begin{array}{l}\left\{ \begin{array}{l}b = 6a\\3a - b = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6a\\3a - 6a = - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = 6a\\a = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6\\a = 1\end{array} \right.\end{array}\)
Vậy parabol là \(y = {x^2} + 6x + 4\).
L
0
5 tháng 9 2019
a) Có thể xảy ra 3 trường hợp :
- Tường hợp 1 : Hai số tự nhiên có thể bằng nhau
-Trường hợp 2 : Số tự nhiên của An có thể lớn hơn
-Trường hợp 3 : Số tự nhiên của Bình có thể lớn hơn
b) Giống như phần a)
# Chúc bạn hok tốt #
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Ta có: \(a = 3,b = 4 \Rightarrow c = \sqrt {{3^2} + {4^2}} = 5\)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
b) Ta có: \(a = 6;b = 5 \Rightarrow c = \sqrt {{6^2} + {5^2}} = \sqrt {61} \)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - \sqrt {61} ;0} \right),{F_2}\left( {\sqrt {61} ;0} \right)\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Theo giả thiết, hai điểm \(A(1;1)\) và \(B( - 1;0)\) thuộc parabol \(\left( P \right):y = a{x^2} + bx + 3\) nên ta có: \(\left\{ {\begin{array}{*{20}{c}}{a + b + 3 = 1}\\{a - b + 3 = 0}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{{ - 5}}{2}}\\{b = \frac{1}{2}}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là: \(y = - \frac{5}{2}{x^2} + \frac{1}{2}x + 3.\)
b) Parabol nhận \(x = 1\) làm trục đối xứng nên \( - \frac{b}{{2a}} = 1\,\, \Leftrightarrow \,\,b = - 2a.\)
Điểm \(M(1;2)\) thuộc parabol nên \(a + b + 3 = 2\,\, \Leftrightarrow \,\,a + b = - 1.\)
Do đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{b = - 2a}\\{a + b = - 1}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là: \(y = {x^2} - 2x + 3\)
c) Parabol có đỉnh \(I(1;4)\) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{ - \frac{b}{{2a}} = 1}\\{a + b + 3 = 4}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{b = - 2a}\\{a + b = 1}\end{array}\,\, \Leftrightarrow \,\,} \right.} \right.\left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = 2}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^2} + 2x + 3.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Phương trình \({x^2} - 2 = 0\) có hai nghiệm là \(\sqrt 2 \) và \( - \sqrt 2 \), nên \(A = \{ \sqrt 2 ; - \sqrt 2 \} \)
Tập hợp \(B = \{ x \in \mathbb{R}|2x - 1 < 0\} \) là tập hợp các số thực \(x < \frac{1}{2}\)
Từ đó \(A \cap B = \{ - \sqrt 2 \} .\)
b) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1,y = - x + 5\} \)
Tức là \(A \cap B\)là tập hợp các cặp số (x; y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}y = 2x - 1\\y = - x + 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2x - 1 = - x + 5\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy \(A \cap B = \{ (2;3)\} .\)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
\(A \cap B\) là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi.
Một tứ giác bất kì thuộc \(A \cap B\) thì nó là hình chữ nhật và có 2 cạnh kề bằng nhau (hình vuông)
Do đó \(A \cap B\) là tập hợp các hình vuông.