Cho hàm số y = a x 2 (a ≠ 0)
b)Vẽ đồ thị của hàm số ứng với giá trị a vừa tìm được ở câu trên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 7 2018
Khi a = 2 thì ta có hàm số: y = x + 2
Khi a = 1,5 thì ta có hàm số: y = 0,5x + 1,5
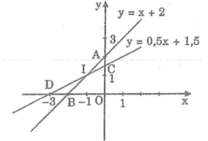
*Vẽ đồ thị của hàm số y = x + 2
Cho x = 0 thì y = 2. Ta có: A(0; 2)
Cho y = 0 thì x = -2. Ta có: B(-2; 0)
Đường thẳng AB là đồ thị hàm số y = x + 2
*Vẽ đồ thị hàm số y = 0,5x + 1,5
Cho x = 0 thì y = 1,5. Ta có: C(0; 1,5)
Cho y = 0 thì x = -3. Ta có: D(-3; 0)
Đường thẳng CD là đồ thị hàm số y = 0,5x + 1,5.
*Tọa độ giao điểm của hai đường thẳng:
Gọi I( x 1 ; y 1 ) là tọa độ giao điểm của hai đường thẳng.
Ta có: I thuộc đường thẳng y = x + 2 nên y 1 = x 1 + 2
I thuộc đường thẳng y = 0,5x + 1,5 nên y 1 = 0,5 x 1 + 1,5
Suy ra: x 1 + 2 = 0,5 x 1 + 1,5 ⇔ 0,5 x 1 = -0,5 ⇔ x 1 = -1
x 1 = -1 ⇒ y 1 = -1 + 2 = 1
Vậy tọa độ giao điểm của hai đường thẳng là I(-1; 1)
28 tháng 6 2018
y=mx+2 (1)
a) Thay x=1 và y=6 vào hs (1)
Ta được: 6=m+2 =>m=4
b) Xét hs y=4x+2
| x | 0 | -1/2 |
| y | 2 | 0 |
| Điểm | B | C |
Xét hs y=2x+1
| x | 0 | -1/2 |
| y | 1 | 0 |
| Điểm | D | E |
Câu b này bn tự vẽ hình mk ko bt gửi ảnh .
c) có phải tìm hoành độ giao đểim ko
27 tháng 3 2015
a) Đồ thị hs đi qua A(1;1) => 1 = m.|1 | + 2.1 => 1 = m + 2 => m = -1
Vậy với m = -1 đồ thị hs đã cho đi qua A(1;1)
b) Với m = -1 => y = -|x| + 2x
Với x \(\ge\) 0 => |x| = x => y = -x + 2.x = x
Với x \(\le\) 0 => |x| = -x => y = -(-x) + 2x = 3x
Vậy vẽ đồ thị hàm số đa cho ta vẽ đường thẳng y = x và y = 3x. Sau đó lấy phần đường thẳng y = x nằm bên phải trục tung và phần đường thẳng y - 3x nằm bên trái trục tung
O x y 1 1 3 y=x y=3x
14 tháng 1 2022
Bài 9:
b: Điểm A thuộc đồ thị vì \(y_A=4=-2\cdot\left(-2\right)=-2\cdot x_A\)
Bài 10:
a: Thay x=1 và y=-3 vào (d), ta được:
\(a\cdot1=-3\)
hay a=-3
22 tháng 1 2022
a: Thay x=1 và y=-2 vào y=ax, ta được:
1xa=-2
hay a=-2
31 tháng 8 2021
a: Thay x=0 và y=2 vào (d), ta được:
a=2
b: Thay x=-1 và y=0 vào (d), ta được:
\(-\left(a-2\right)+a=0\)
\(\Leftrightarrow2=0\)(vô lý)
b) Bảng giá trị:
Đồ thị hàm số y = 1/2 x 2 là một đường Parabol nằm phía trên trục hoành, nhận trục tung làm trục đối xứng, nhận gốc tọa độ O(0;0) làm đỉnh và là điểm thấp nhất.