Kim tự tháp là một khối đa diện thuộc hình: A. hình lăng trụ đều ...

M

Monlee2k8

4 tháng 11 2021

Kim tự tháp là một khối đa diện thuộc hình: A. hình lăng trụ đều B. hình chóp đều C. hình hộp chữ nhật D. hình nón cụt ...

Đọc tiếp

#Công nghệ lớp 8

1

PK

Phùng Kim Thanh

4 tháng 11 2021

B

Đúng(0)

MH

Minh Hiếu Vũ

26 tháng 10 2021

Kim tự tháp là một khối đa diện thuộc hình

A. hình hộp chữ nhật.

B. hình nón cụt.

C. hình lăng trụ đều.

D. hình chóp đều.

#Công nghệ lớp 8

9

....

26 tháng 10 2021

c

Đúng(1)

OY

OH-YEAH^^

26 tháng 10 2021

D

Đúng(0)

TT

Trần Tuấn Long

29 tháng 10 2021

Khái niệm các khối đa diện (hình hộp chữ nhật, hình lăng trụ, hình chóp đều) và các khối tròn xoay (hình trụ, hình nón, hình cầu). Đặc điểm hình chiếu của các khối đa diện và khối tròn xoay.

#Công nghệ lớp 8

2

T

tholauyeu

29 tháng 10 2021

- Hình hộp chữ nhật là hình được bao bọc bởi sáu hình chữ nhật

- Hình lăng trụ là hình đều được bao bởi 2 mặt đáy là 2 hình đa giác đều bằng nhau và các mặt bên là các hình chữ nhật bằng nhau

-hình chóp đều được bao bởi mặt đáy là một hình đa giác đều và các mặt bên là các hình tam giác cân bằng nhau có chung đỉnh

- Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình trụ

- Khi quay hình tam giác vuông một vòng quay đường kính cố định, ta được hình cầu

- Khi quay tam giác vuông một vòng quanh góc vuông cố định, ta được hình nón

Đúng(2)

WT

Wibu Team

7 tháng 11 2021

Hay

Đúng(0)

DT

Đinh Thảo Hiền

16 tháng 10 2021

4. Nêu định nghĩa khối đa diện, hình hộp chữ nhật, hình lăng trụ đều, hình chóp đều.

#Công nghệ lớp 8

1

LS

Long Sơn

16 tháng 10 2021

Tham khảo:

1.Hình hộp chữ nhật:Được tạo bởi 6 hình chữ nhật

Hình chiếu :

Hình	Hình chiếu	Hình dạng	Kích thước
1	Đứng	Chữ nhật	Chiều dài,chiều cao
2	Bằng	Chữ nhật	Chiều dài ,chiều rộng
3	Cạnh	Chữ nhật	Chiều cao ,chiều rộng

2.Hình lăng trụ đều: Được tạo bởi 2 mặt đáy là 2 hình đa giác đều bằng nhau và các mặt bên là hình chữ nhật bằng nhau

Hình chiếu

Hình	Hình chiếu	Hình dạng	Kích thước
1	Đứng	Chữ nhật	Chiều dài,cạnh đáy,chiều cao
2	Bằng	Tam giác	Chiều dài,cạnh đấy,chiều cao đáy
3	Cạnh	Chữ nhật	Chiều cao

3.Hình chóp đều: Được tạo bởi mặt đáy là hình đa giác đều và các mặt bên là hình tam giác cân bằng nhau có chung đỉnh

Hình chiếu

Hình	Hình chiếu	Hình dạng	Kích thước
1	Đứng	Tam giác	Chiều dài canh đáy,chiều cao hình chóp
2	Bằng	Hình vuông	Chiều dài cạnh đáy
3	Cạnh	Tam giác	Chiều dài canh đáy,chiều cao hình chóp

4. Hình nón:Hình nón được tạo thành khi quay hình tam giác vuông một vòng quanh một cạnh góc vuông cố định ta được hình nón

Đúng(0)

PT

Pham Trong Bach

8 tháng 1 2018

Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150m, cạnh đáy dài 220m. Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu? ( Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên). ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

8 tháng 1 2018

Đúng(0)

PT

Pham Trong Bach

10 tháng 11 2019

Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150 m cạnh đáy dài 220 m . Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu? ( Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên). A. 220 346 m 2 B. 1100 346 m 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

10 tháng 11 2019

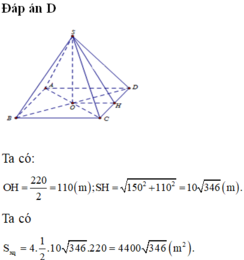
Đáp án D

Ta có: O H = 220 2 = 110 m ; S H = 150 2 + 110 2 = 10 346 m .

Ta có S x q = 4. 1 2 .10 346 .220 = 4400 346 m 2 .

Đúng(0)

PT

Pham Trong Bach

24 tháng 10 2019

Khẳng định nào sau đây sai?

A. Hình lập phương là đa diện lồi.

B. Tứ diện là đa diện lồi.

C. Hình hộp là đa diện lồi.

D. Hình tạo bởi hai khối lăng trụ có chung nhau một mặt bên là một hình đa diện lồi.

#Toán lớp 12

1

CM

Cao Minh Tâm

24 tháng 10 2019

Chọn D.

Hình tạo bởi hai khối lăng trụ lục giác đều bằng nhau có chung nhau một mặt bên không phải là hình đa diện lồi.

Đúng(0)

PT

Pham Trong Bach

8 tháng 12 2019

Kim tự tháp Kê-ốp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231 m. Tính cạnh bên và diện tích một mặt bên của kim tự tháp.

#Toán lớp 8

1

CM

Cao Minh Tâm

8 tháng 12 2019

Đúng(0)

PT

Pham Trong Bach

22 tháng 10 2017

Cho hình trụ (T) có chiều cao h = 2 m , bán kính đáy r = 3 m . Giả sử (L) là hình lăng trụ đều n cạnh có hai đáy là đa giác đều nội tiếp đường tròn đáy của hình trụ (T). Khi n tăng lên vô hạn thì tổng diện tích tất cả các mặt của của khối lăng trụ (L) (tính bằng m 2 ) có giới hạn là: ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

22 tháng 10 2017

Đúng(0)

PT

Pham Trong Bach

29 tháng 12 2018

Kim tự tháp Kê-ôp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231m. Tính diện tích xung quanh và thể tích của kim tự tháp

#Toán lớp 8

2

CM

Cao Minh Tâm

29 tháng 12 2018

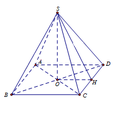
Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.

Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.

Tính được:

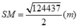
Diện tích xung quanh của kim tự tháp là:

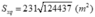
Thể tích của kim tự tháp:

V = 2436819 (m³)

Đúng(0)

74

789 456

23 tháng 4

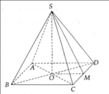
Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.

1. **Tính cạnh bên**:
Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.

Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:

\[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]

\[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]

\[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]

\[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]

\[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]

2. **Tính diện tích một mặt bên**:
Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:

\[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]

Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:

\[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]

\[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]

\[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]

Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).

Đúng(0)

PT

Pham Trong Bach

16 tháng 10 2019

Lăng trụ A B C . A ' B ' C ' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A ' lên (ABC) trùng với tâm O của tam giác ABC. Mặt phẳng (P) chứa BC vuông góc với A A ' cắt lăng trụ theo thiết diện có diện tích bằng a 2 3 8 . Thể tích khối đa diện A A C ' B A ' ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

16 tháng 10 2019

Đáp án D

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP